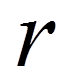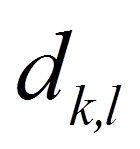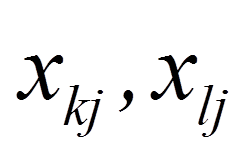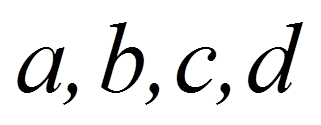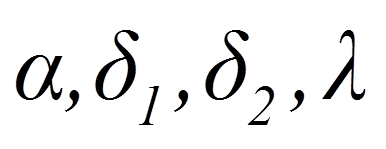Clusteranalyse
Seiteninhalt
- Quick Start
- 1. Einführung
- 1.1. Beispiele für Fragestellungen
- 1.2. Voraussetzungen der Clusteranalyse
- 2. Grundlegende Konzepte
- 2.1. Beispiel einer Studie
- 2.2. Wahl eines Proximitätsmasses
- 2.3. Wahl des Clustering-Algorithmus
- 3. Clusteranalyse mit SPSS
- 3.1. SPSS-Befehle
- 3.2. Prozess der Clusterbildung
- 3.3. Bestimmen der Anzahl Cluster
- 3.4. Beschreibung der Cluster
- 3.5. Eine typische Aussage
Quick Start
1. Einführung
Die Clusteranalyse gruppiert Untersuchungsobjekte zu natürlichen Gruppen (sogenannten "Clustern").
Bei den Untersuchungsobjekten kann es sich sowohl um Individuen (z.B. befragte Personen), Gegenstände (z.B. Fahrzeuge, Haarbürsten) als auch um Länder oder Organisationen handeln. Durch die Anwendung clusteranalytischer Verfahren können diese Objekte anhand ihrer Eigenschaften (z.B. Geschlecht, Lohnklasse, Fahrzeugklasse) zu Clustern zusammengefasst werden. Dabei soll jedes Cluster in sich möglichst homogen sein, während sich die Cluster möglichst stark voneinander unterscheiden sollen.
Clusteranalytische Verfahren haben explorativen Charakter, da man keine inferenzstatistischen Rückschlüsse auf die Grundgesamtheit macht, sondern datengetrieben eine Struktur zu entdecken versucht. Die Forschenden spielen hierbei eine wichtige Rolle, da das Ergebnis unter anderem von der Wahl des Proximitätsmasses und des Clustering-Algorithmus beeinflusst wird. Das Ergebnis einer Clusteranalyse sind Cluster von Objekten, die beschrieben (und oft auch verglichen) werden – wie beispielsweise Lebensstilgruppen oder Konsumentensegmente.
Die Fragestellung der Clusteranalyse wird oft wie folgt verkürzt:
"Können die Untersuchungsobjekte zu natürlichen Gruppen (Clustern) zusammengefügt werden?"
1.1. Beispiele für Fragestellungen
- Können mittels Jahreseinkommen, Alter und Berufserfahrung Cluster gebildet werden?
- Können Personen anhand ihres Markenbewusstseins, ihres Umweltbewusstseins und ihrer politischen Orientierung gruppiert werden?
- Lassen sich Sportler in Cluster unterteilen durch die Variablen "Häufigkeit des Ausdauertrainings", "Dauer des Ausdauertrainings", "Körpergewicht" und "Lungenvolumen"?
1.2. Voraussetzungen der Clusteranalyse
| ✓ | Wenn auf die Grundgesamtheit rückgeschlossen werden sollen, muss die Stichprobe genügend gross sein. In der Praxis werden oft sehr kleine Stichproben verwendet. |
| ✓ | Fehlende Werte müssen vor dem Durchführen einer Clusteranalyse bereinigt werden, wofür es unterschiedliche Methoden gibt (Ausschliessen der Fälle mit fehlenden Werten, fehlende Werte durch Mittelwert ersetzen, fehlende Werte imputieren). |
| ✓ | Zur Analyse mit SPSS müssen die Skalenniveaus aller Variablen, die zur Clusterbildung verwendet werden, auf demselben Niveau sein. Ist dies nicht der Fall, so werden oftmals alle Variablen auf das tiefste auftretende Skalenniveau transformiert. |
| ✓ | Weisen die Variablen grosse Unterschiede bezüglich ihres Wertebereichs auf, so werden die Variablen oft z-transformiert. |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
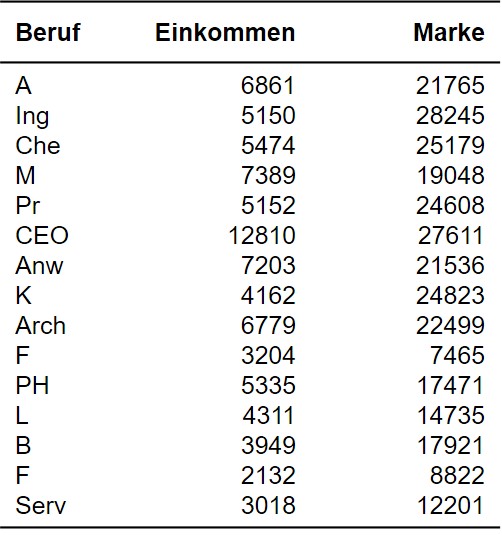
Ein Markforschungsinstitut möchte 15 Berufe anhand der Kriterien Einkommen und Markenbewusstsein in Gruppen einteilen. Wie viele Cluster ergeben sich? Wie lassen sich diese interpretieren?
Der zu analysierende Datensatz (siehe Abbildung 1) enthält für jeden der 15 Berufe (Beruf) das Einkommen (Einkommen) sowie einen Wert für das Markenbewusstsein (Marke).
2.2. Wahl eines Proximitätsmasses
Während der eigentlichen Clusterbildung wird nach gewissen Regeln entschieden, wie die Objekte oder Cluster bestimmt werden, die zusammengeschlossen werden sollen. Das Ergebnis dieses Prozesses hängt nicht nur von der Wahl des Clustering-Algorithmus ab, sondern auch davon, wie die Distanz oder Ähnlichkeit zwischen den Objekten bestimmt wird. Zu Beginn der Clusteranalyse wird daher in Abhängigkeit von der Skalierung der Variablen ein sogenanntes "Proximitätsmass" gewählt. Proximitätsmasse sind ein Mass für die Ähnlichkeit oder Distanz der zu clusternden Objekte. Daher werden an dieser Stelle exemplarisch einige Masse für binäre Variablen und einige für intervallskalierte Variablen betrachtet.
Proximitätsmasse für intervallskalierte Variablen
Bei intervallskalierten Variablen wird sehr oft die quadrierte Euklidische Distanz als Distanzmass verwendet. Dabei handelt es sich um die quadrierte "Luftliniendistanz". Daneben gibt es weitere Masse, wie beispielsweise die Euklidische Distanz (einfache "Luftliniendistanz") oder die sogenannte "City-Block-Distanz".
Viele der Proximitätsmasse für intervallskalierte Daten können durch die sogenannte Minkowski-Metrik abgebildet werden:
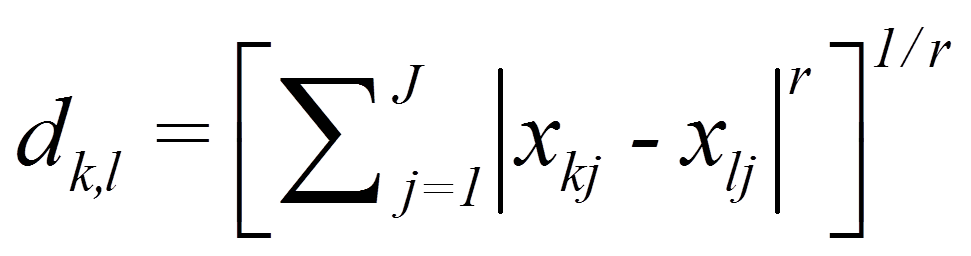
mit
|
|
= | Minkowski-Konstante |
|
|
= | Distanz zwischen den Objekten k und l (z.B. Distanz zwischen Versuchspersonen 1 und 2) |
|
|
= | Anzahl Clustervariablen (wie viele Variablen zur Clusterbildung verwendet werden) |
|
|
= | Variablenwerte j der Objekte k und l |
Beträgt die Minkowski-Konstante r = 1, so reduziert sich die Formel auf die City-Block-Distanz. Bei r = 2 wird die Euklidische Distanz berechnet.
Proximitätsmasse für binäre Variablen
Eine Reihe von Proximitätsmassen für binäre Variablen wird auf der Basis von Vergleichen gebildet. Hierbei wird die Ähnlichkeit/Unähnlichkeit von zwei Objekten betrachtet.
In Abbildung 2 ist ein Beispiel aufgeführt. Die zwei zu vergleichenden Objekte sind ein Mercedes und ein BMW. Diese beiden Fahrzeuge werden anhand von fünf Merkmalen, wie beispielsweise ABS, verglichen. Es wird bei beiden Fahrzeugen jeweils geprüft, ob ein bestimmtes Merkmal vorhanden ist (= 1) oder nicht (= 0). Es gibt vier mögliche Fälle (in der Zeile "Fall" mit A, B, C oder D bezeichnet:
- Beide Autos weisen eine bestimmte Eigenschaft auf (A)
- Der BMW weist eine bestimmte Eigenschaft auf, der Mercedes nicht (B)
- Der Mercedes weist eine bestimmte Eigenschaft auf, der BMW nicht (C)
- Keines der Autos weist eine bestimmte Eigenschaft auf (D)
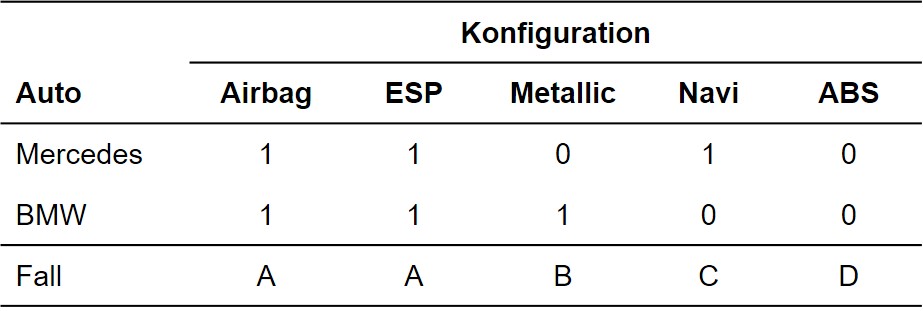
Im Beispiel tritt Fall A zweimal auf, während B, C und D je einmal vorliegen. Basierend auf diesen Häufigkeiten lassen sich verschiedene Proximitätsmasse berechnen. Diese unterscheiden sich darin, wie die verschiedenen Fälle gewichtet werden. Die verallgemeinerte Formel lautet:
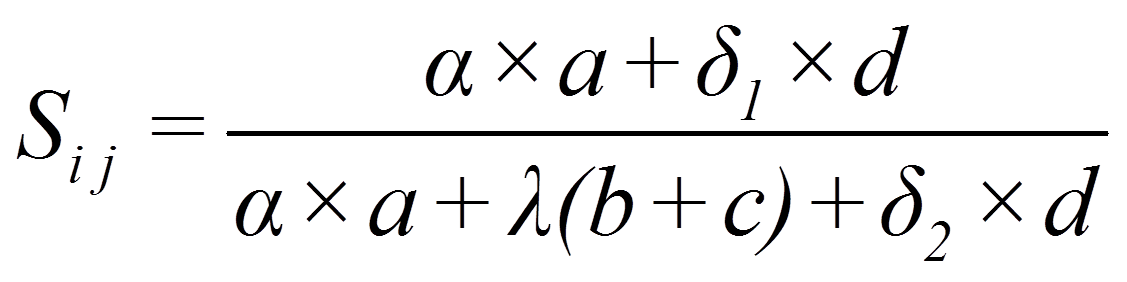
mit
|
|
= | Objekte |
|
|
= | Häufigkeit, mit der ein bestimmter Fall vorkommt (a für A, b für B, c für C, d für D) |
|
|
= | Anzahl Clustervariablen (wie viele Variablen zur Clusterbildung verwendet werden) |
Die Gewichte α, δ1, δ2 und λ werden je nach Proximitätsmass anders gewählt. Inhaltlich entscheiden diese Gewichte darüber, ob und inwiefern die Fälle A, B, C und D berücksichtigt werden. Erhöht beispielsweise die Tatsache, dass beide Autos kein ABS aufweisen (Fall D), ihre Ähnlichkeit?
Bei "Einfacher Übereinstimmung" ("Simple Matching") erhöht D die Ähnlichkeit:
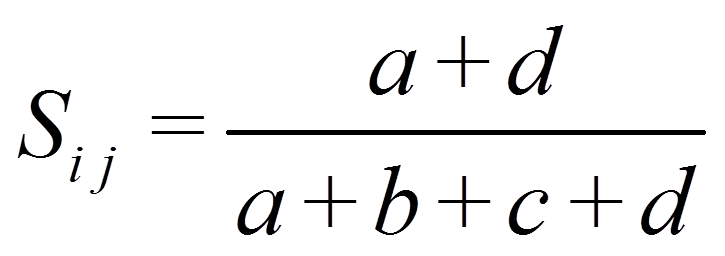
Für das Beispiel ergibt dies:
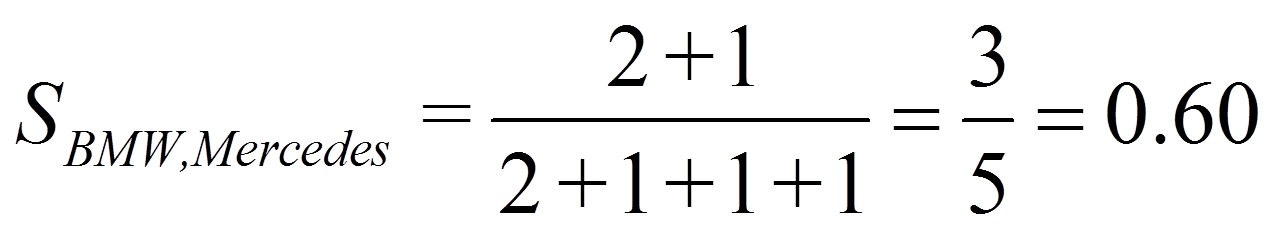
Beim Proximitätsmass nach Russel & Rao dagegen reduziert D die Ähnlichkeit:
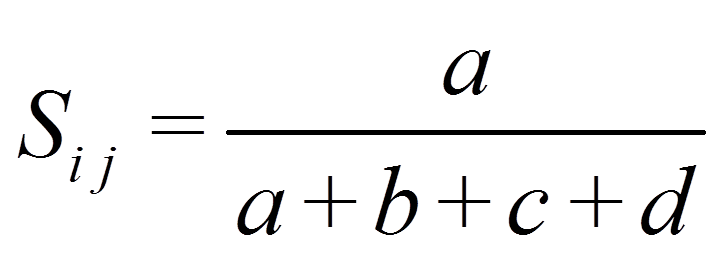
Für das Beispiel ergibt dies:
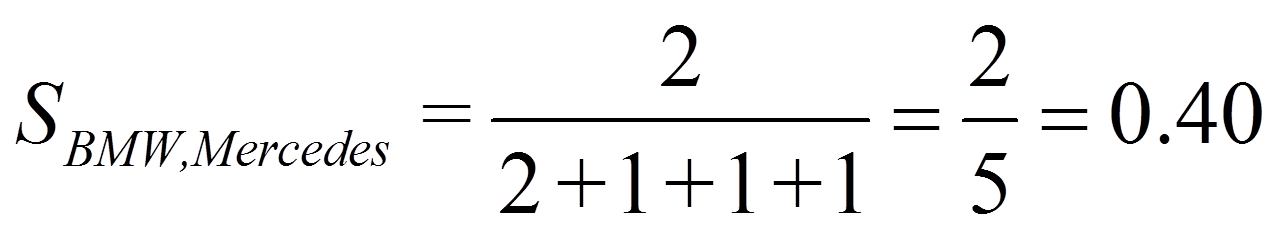
Bei "Dice" wird D nicht berücksichtigt, während A stärker gewichtet wird:
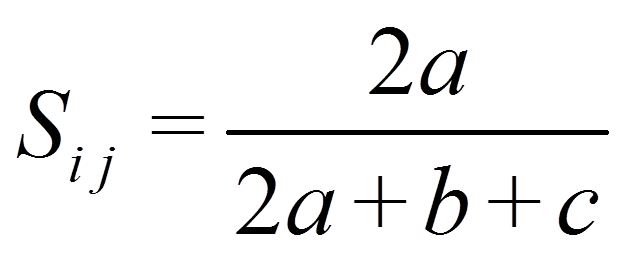
Für das Beispiel ergibt dies:
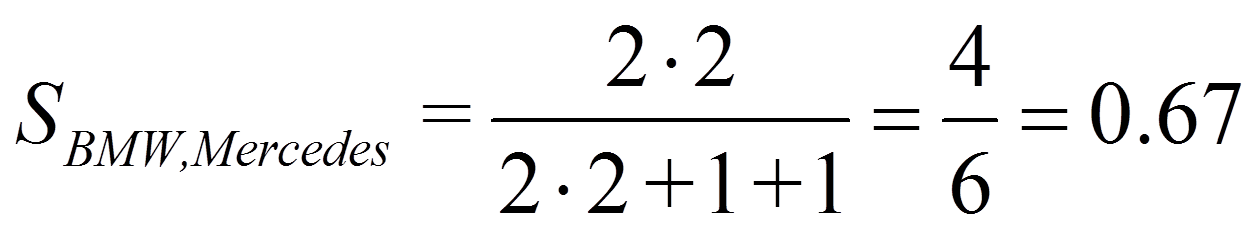
Bei den hier beschriebenen Massen handelt es sich lediglich um eine kleine Auswahl. Die Entscheidung für ein bestimmtes Mass wird in der Praxis aufgrund inhaltlicher Überlegungen (Was sollte hoch gewichtet werden?) sowie der Forschungstradition getroffen.
2.3. Wahl des Clustering-Algorithmus
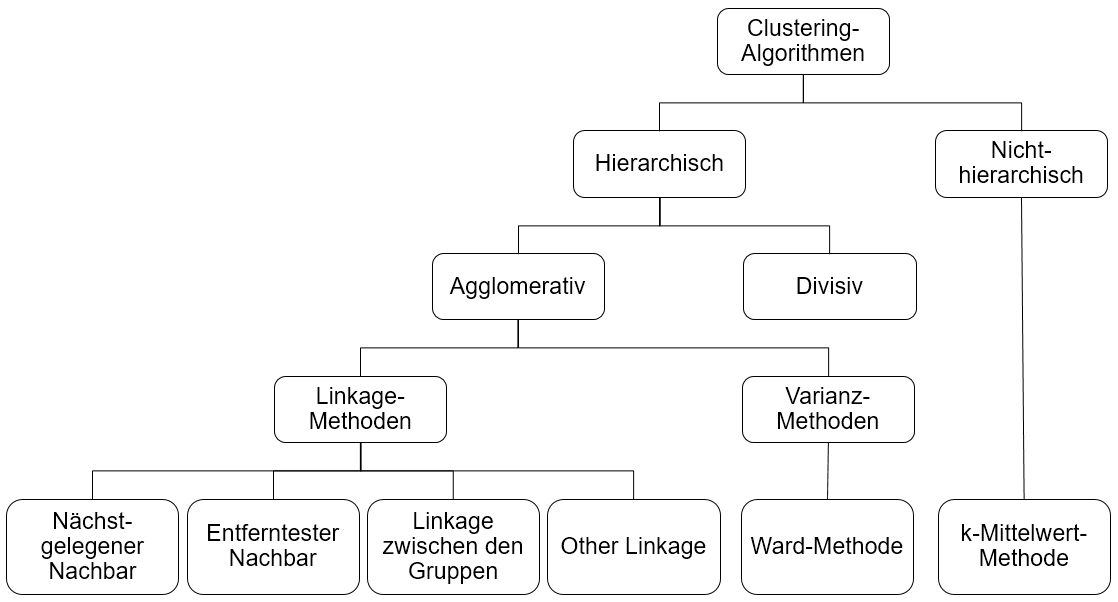
Zunächst wird zwischen hierarchischen und nicht-hierarchischen Algorithmen unterschieden. Im Rahmen dieser Einführung werden ausschliesslich hierarchische Algorithmen behandelt. Diese werden in agglomerative und divisive Verfahren unterteilt. Bei divisiven Verfahren wird zunächst ein Cluster gebildet, das alle Datenpunkte enthält. Dieses wird sodann schrittweise in kleinere Cluster zerteilt, bis jeder Fall ein eigenes Cluster bildet. Bei agglomerativen Verfahren hingegen werden die Datenpunkte zuerst einzeln betrachtet und dann schrittweise zu Clustern zusammengefasst.
Die agglomerativen Verfahren wiederum werden in Linkage-Methoden und Varianz-Methoden unterteilt. Bei den Linkage-Methoden wird in jedem Schritt geprüft, welche der Cluster sich am nächsten liegen. Diese werden fusioniert. Je nach Linkage-Methode wird diese Distanz zwischen den Clustern unterschiedlich bestimmt:
- Nächstgelegener Nachbar (engl. "single linkage"): Das Minimum aller möglichen Distanzen zwischen den Datenpunkten in Cluster 1 und jenen in Cluster 2 wird betrachtet.
- Entferntester Nachbar (engl. "complete linkage"): Das Maximum aller möglichen Distanzen zwischen den Datenpunkten in Cluster 1 und jenen in Cluster 2 wird betrachtet.
- Linkage zwischen Gruppen (engl. "average linkage"): Der Mittelwert aller möglichen Distanzen zwischen den Datenpunkten in Cluster 1 und jenen in Cluster 2 wird betrachtet.
- Other Linkage: Dies umfasst verschiedene Methoden, beispielsweise wird die Distanz zwischen dem Median von Cluster 1 und dem Median von Cluster 2 betrachtet (Median-Clustering).
Die Ward-Methode ist die am häufigsten verwendete Varianz-Methode. Dabei wird für jedes Cluster die Summe der quadrierten Distanzen der Einzelfälle vom jeweiligen Cluster-Zentroiden berechnet. Diese Werte werden aufsummiert. Im nächsten Schritt werden jeweils jene zwei Cluster fusioniert, deren Zusammenfügen die geringste Erhöhung der Gesamtsumme der quadrierten Distanzen zur Folge hat.
Im folgenden Beispiel wird die Ward-Methode angewandt.
3. Clusteranalyse mit SPSS
3.1. SPSS-Befehle
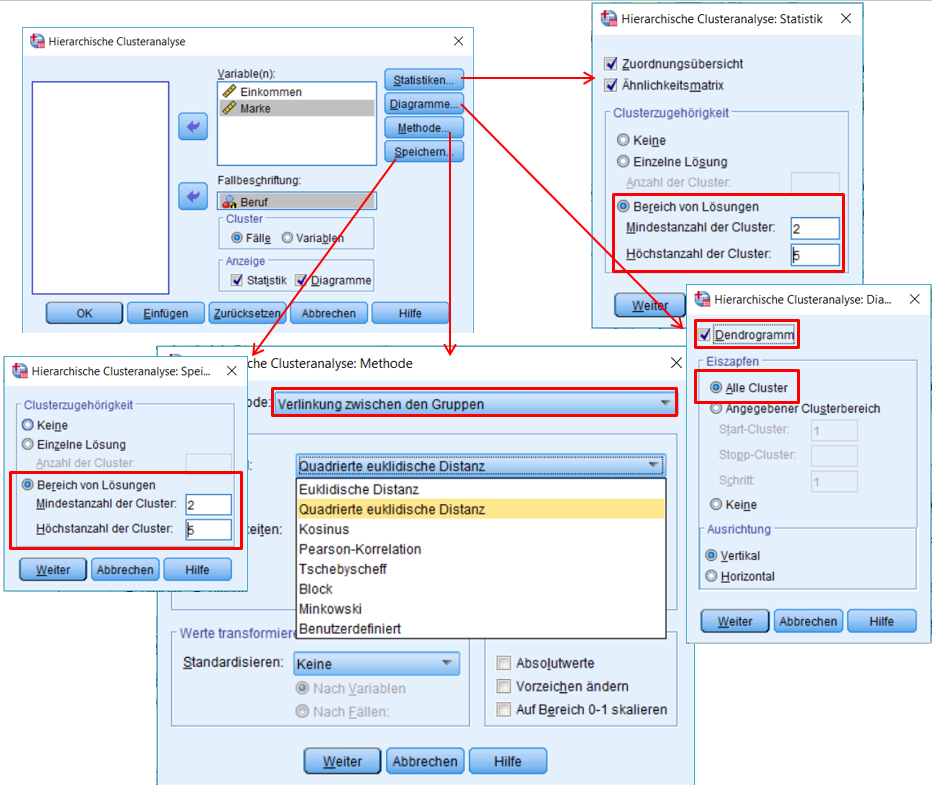
SPSS-Menü: Analysieren > Klassifizieren > Hierarchische Cluster
Hinweise
- Im Feld Fallbeschriftung kann eine Variable eingegeben werden, die zur Beschriftung der Fälle verwendet werden soll. In diesem Fall ist es sinnvoll, dazu Beruf zu verwenden (Syntax "/ID=Beruf").
- Unter Methode werden der Clustering-Algorithmus (Cluster-Methode) und das Proximitätsmass (unter Messniveau) gewählt. Die Wahl des Proximitätsmasses ist abhängig von Datentyp, weswegen unter Messniveau die Skalierung der Daten angegeben werden muss.
- Sollen die Variablen standardisiert werden, bevor sie für das Clustering verwendet werden, so kann dies unter Methode festgelegt werden (Standardisieren: Z-Werte). Alternativ können die Variablen vorab standardisiert und gespeichert werden:
Analysieren > Deskriptive Statistik > Deskriptive Statistik…
SPSS-Syntax
CLUSTER Einkommen Marke
/METHOD WARD
/MEASURE= SEUCLID
/ID=Beruf
/PRINT SCHEDULE CLUSTER(2,5)
/PRINT DISTANCE
/PLOT DENDROGRAM VICICLE
/SAVE CLUSTER(2,5).
Beim Eingeben der gewünschten Einstellungen in SPSS sollte beachtet werden, dass die Standardeinstellung des Proximitätsmasses (Quadrierte Euklidische Distanz) sich für die folgenden Clustering-Algorithmen eignet: Linkage zwischen Gruppen (BAVERAGE), Other Linkage (CENTROID oder MEDIAN) und die Ward-Methode (WARD).
Des Weiteren ist es hilfreich, unter "Statistiken" bei "Cluster-Zugehörigkeit" anzugeben, wie viele Cluster in etwa möglich sein könnten, beispielsweise 2 bis 5 wie hier im Beispiel. Dies verändert die Berechnung nicht, sondern fügt lediglich die (sehr nützliche) Tabelle "Clusterzugehörigkeit" zur Ausgabe hinzu (Abbildung 8). Diese zeigt, welche Untersuchungsobjekte zu welchem Cluster gehören – gegeben es liegen 2, 3, 4 oder 5 Cluster vor.
Diese Clusterzughörigkeit lässt sich zudem im Datensatz speichern. Dazu kann bei "Speichern" ebenfalls ein Bereich von Lösungen angegeben werden. Im Beispiel wurde 2 bis 5 gewählt, wie die letzte Zeile der Syntax zeigt ("/SAVE CLUSTER(2,5)"). Durch diese Wahl werden im Datensatz die folgenden Variablen hinzugefügt: CLU2_1 (Zugehörigkeit bei 2 Clustern), CLU3_1 (bei 3 Clustern), CLU4_1 (bei 4 Clustern) und CLU5_1 (bei 5 Clustern). Dieses Speichern verändert den Clustering-Prozess nicht, sondern fügt lediglich neue Variablen hinzu. Diese sind später wichtig für die Beschreibung und Darstellung der Cluster.
3.2. Prozess der Clusterbildung
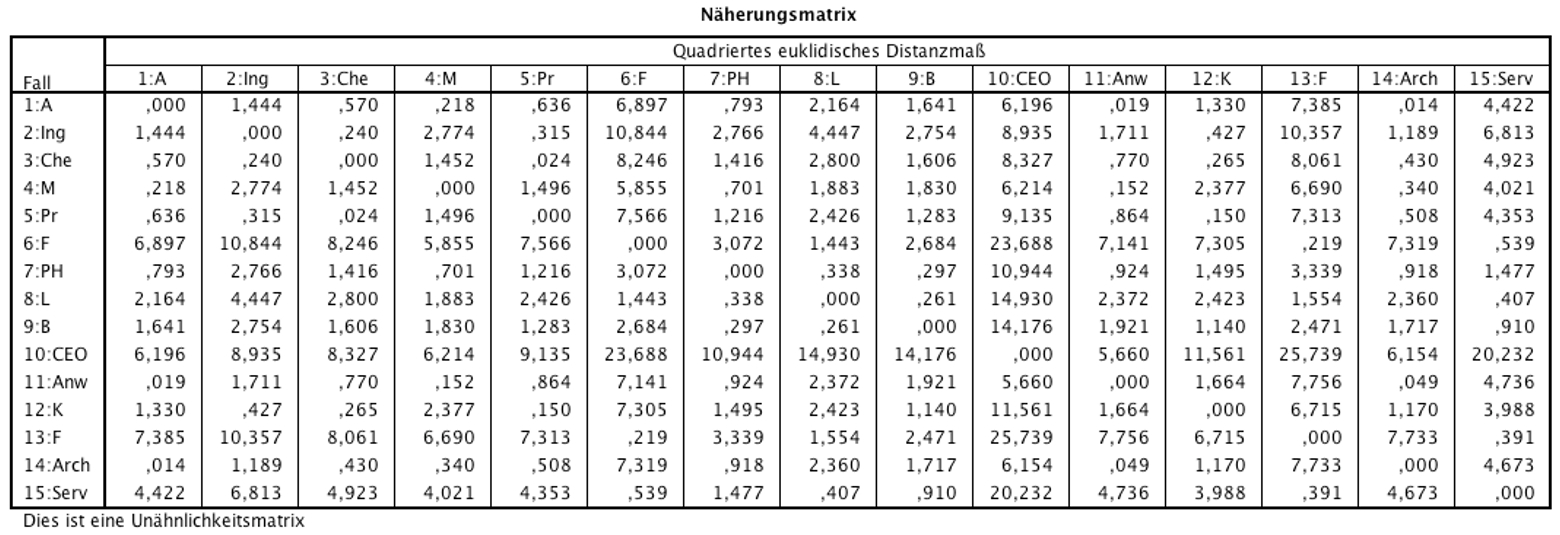
SPSS gibt eine sogenannte "Näherungsmatrix" aus (Abbildung 5). Diese enthält die quadrierten Euklidischen Distanzen. Für jede Kombination von Datenpunkten lässt sich die quadrierte Euklidische Distanz ablesen. Beispielsweise liegen die Fälle 1 und 2 um 1.444 Einheiten auseinander, während die Fälle 1 und 14 mit einer Distanz von .014 die geringste Distanz aufweisen.
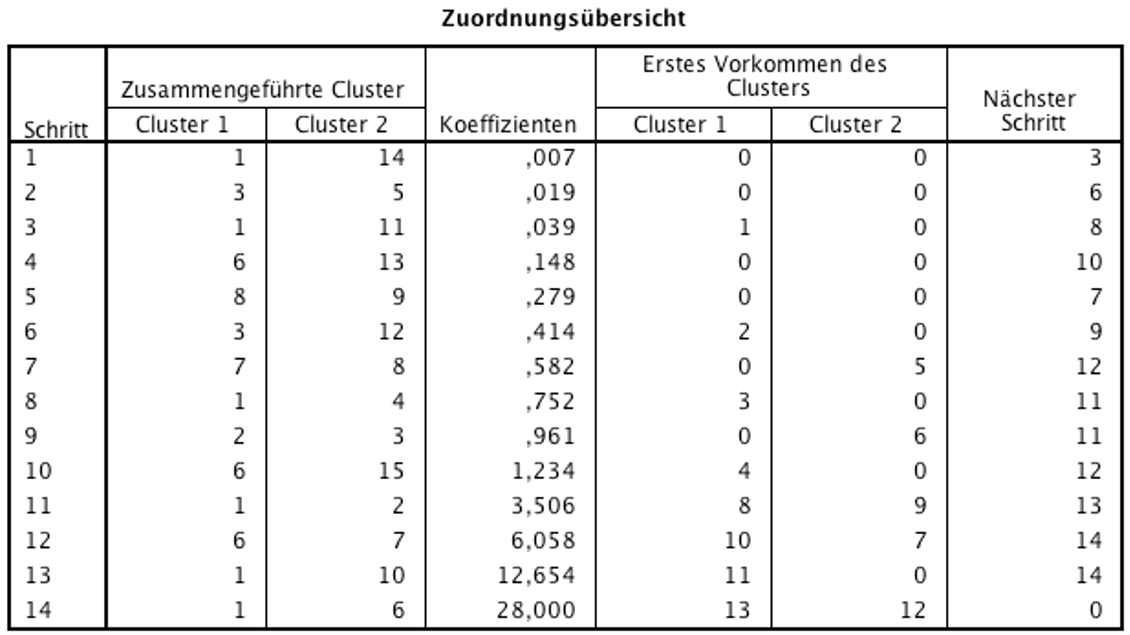
In der "Zuordnungsübersicht" (Abbildung 6) wird dargestellt, wie die Cluster Schritt für Schritt kombiniert werden. Zu Beginn ist jeder Fall in einem eigenen Cluster. In "Schritt 1" werden sodann jene beiden Cluster zusammengefügt, die sich am nächsten liegen. Dies sind die Datenpunkte 1 und 14. Dieses neue Cluster (1, 14) wiederum wird in Schritt 3 mit dem Datenpunkt 11 geclustert. Dadurch entsteht das Cluster (1, 14, 11). Im zweiten Schritt werden die Datenpunkte 3 und 5 zu einem Cluster (3, 5) zusammengefügt.
Die Spalte "Koeffizienten" enthält ein Mass dafür, wie viel Heterogenität bereits in Clustern zusammengefasst wurde. Daher steigt die Grösse des Koeffizienten mit jedem Schritt. Im letzten Schritt (hier "Schritt 14") werden die beiden dann noch verbleibenden Cluster schliesslich verbunden und alle Fälle sind in einem gemeinsamen Cluster.
3.3. Bestimmen der Anzahl Cluster
Zu Beginn der Cluster-Bildung ist jeder Fall in einem eigenen Cluster; am Ende sind alle Fälle in einem grossen Cluster. Daher stellt sich nun die Frage, wo zwischen 15 Clustern und 1 Cluster die optimale Lösung liegt. Von wie vielen Clustern soll ausgegangen werden? Um dies zu beantworten, werden in der Regel inhaltliche Überlegungen berücksichtigt (Was ist sinnvoll?) und es wird auf das sogenannte "Dendrogramm" zurückgegriffen (Abbildung 7).
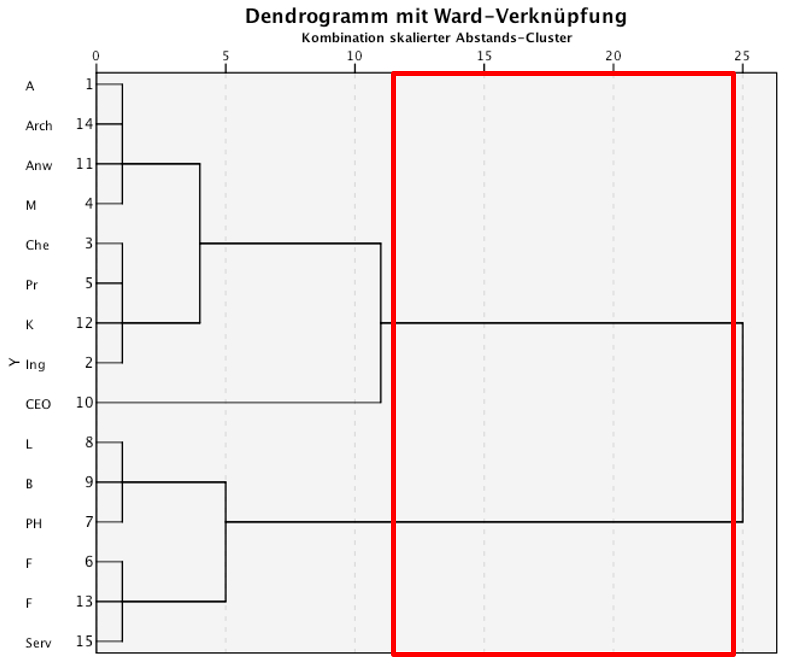
Das Dendrogramm liest sich von links nach rechts und beschreibt in diese Richtung den Prozess des Clusterings. Die horizontale Achse beschreibt Heterogenität. Diese wird in SPSS für diese Abbildung auf den Bereich von 0 bis 25 normiert. Auf der linken Seite des Dendrogramms sind alle Fälle einzeln aufgelistet. Zunächst entspricht jeder Fall einem Cluster, was sich daran zeigt, dass jeder Fall eine "eigene" kurze, horizontale Linie aufweist. Diese Cluster werden von links nach rechts nach und nach zu grösseren Clustern zusammengefügt. Vertikale Linien illustrieren, dass zwei Cluster fusioniert werden.
Die Anzahl Cluster wird in der Regel unter Berücksichtigung des grössten Zuwachses der Heterogenität im Dendrogramm bestimmt. Im Beispiel kommt es zum grössten Heterogenitätszuwachs zwischen einer Drei-Cluster-Lösung und einer Ein-Cluster-Lösung (rote Box in Abbildung 7, links davon besteht eine Drei-Cluster-Lösung, rechts davon einer Ein-Cluster-Lösung). Das heisst, das Dendrogramm legt eine Zwei-Cluster-Lösung nahe. Da dies inhaltlich plausibel ist (davon wird im Rahmen dieses Lehrbeispiels ausgegangen), wird eine Zwei-Cluster-Lösung übernommen.
3.4. Beschreibung der Cluster
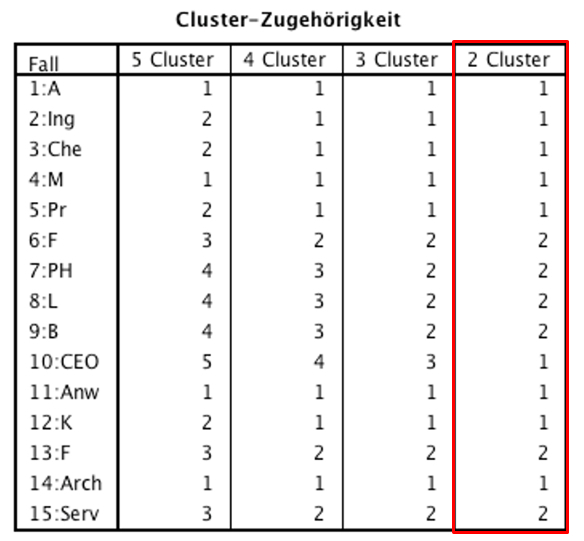
Die Tabelle "Cluster-Zugehörigkeit" (siehe Abbildung 8) zeigt, welche Fälle zu welchem Cluster gehören. Da aufgrund des Dendrogramms eine Zwei-Cluster-Lösung gewählt wurde, wird in Abbildung 8 ausschliesslich jene Spalte betrachtet, welche die Clusterzugehörigkeit bei zwei Clustern zeigt (Spalte "2 Cluster"). Es ist zu erkennen, dass die Fälle 1, 2, 3, 4, 5, 10, 11, 12 und 14 das Cluster 1 bilden und die Fälle 6, 7, 8, 9, 13 und 15 das Cluster 2.
Zur graphischen Darstellung der Cluster kann in SPSS folgendermassen ein Streudiagramm (Scatterplot) erstellt werden:
Grafik > Klassische Dialogfelder > Streu-/Punkt-Diagramm > Einfaches Streudiagramm.
Die unterschiedliche Färbung der Punkte gemäss Clusterzugehörigkeit wird erzielt, indem bei "Markierung festlegen durch" die Variable eingefügt wird, die die Clusterzugehörigkeit enthält (hier: CLU2_1).
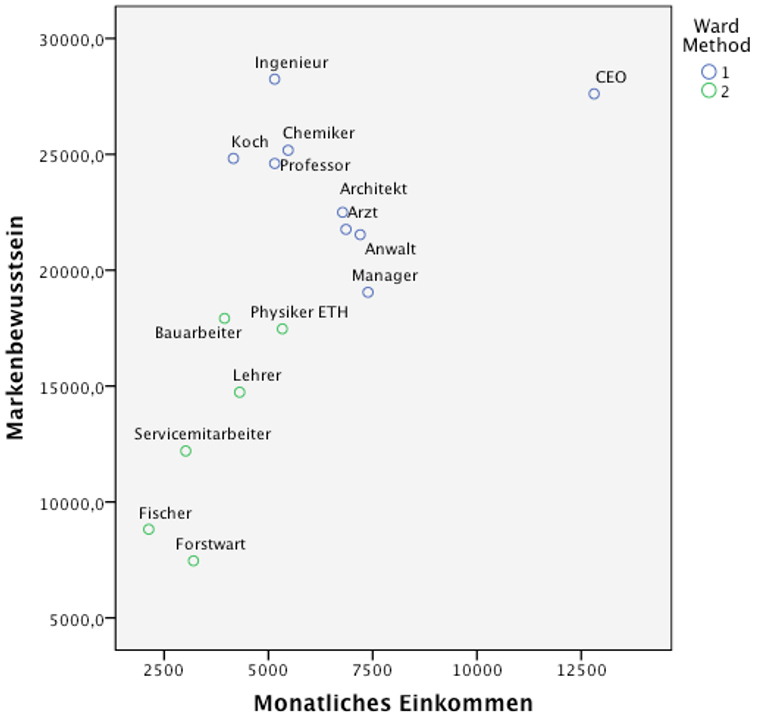
Das Streudiagramm in Abbildung 9 veranschaulicht die Clusterzugehörigkeit der einzelnen Datenpunkte. Es ist zu erkennen, dass "CEO" möglicherweise einen Ausreisser darstellt. Trotzdem wurde "CEO" in Cluster 1 aufgenommen. Eine Alternative wäre, "CEO" in einem separaten Cluster zu belassen (eine Drei-Cluster-Lösung) oder aus der Analyse auszuschliessen. Zur Beschreibung der Cluster werden oftmals deskriptive Statistiken verwendet. Um diese zu erstellen, den Datensatz mittels "Split File" virtuell aufzuteilen. Dies kann im SPSS-Menü durchgeführt werden: Daten > Datei aufteilen. Deskriptive Statistiken werden erstellt über das SPSS-Menü Analysieren > Deskriptive Statistik > Häufigkeiten.
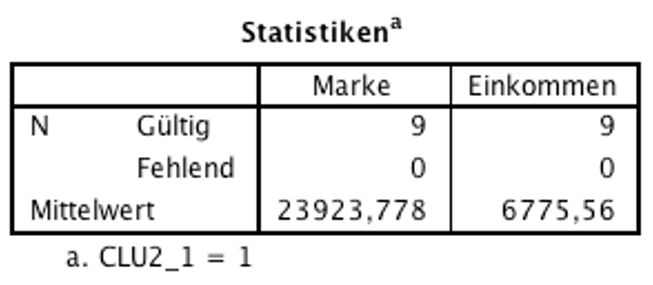
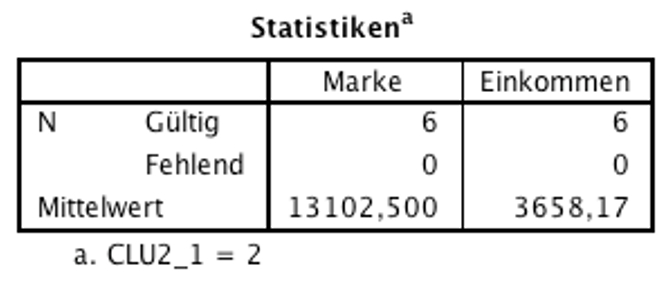
Die deskriptiven Statistiken für Cluster 1 und Cluster 2 (Abbildungen 10 und 11) zeigen die jeweiligen Mittelwerte des Markenbewusstseins und des Einkommens. Von besonderem Interesse für die Interpretation der Cluster sind oft Mittelwertsunterschiede zwischen den Clustern. Um deren Signifikanz zu prüfen, müssten zusätzliche Tests durchgeführt werden, hier beispielsweise t-Tests für unverbundene Stichproben (oder bei mehr als zwei Clustern eine einfaktorielle ANOVA).
3.5. Eine typische Aussage
Die Clusteranalyse hat ergeben, dass die Berufe zwei Cluster bilden (Ward-Methode, quadrierte Euklidische Distanz). Es zeigt sich, dass Personen mit hohem Einkommen markenbewusster sind (Cluster 1). Dazu zählen beispielsweise Personen folgender Berufsgruppen: Ärzte/-innen, Anwälte/-innen und CEOs. Cluster 2 dagegen beschreibt Personen mit niedrigerem Einkommen und geringerem Markenbewusstsein. Es umfasst beispielsweise Lehrer/-innen, Servicemitarbeiter/-innen sowie Fischer/-innen.