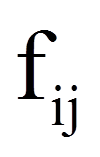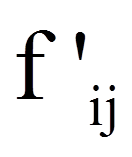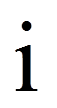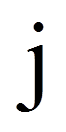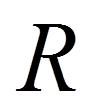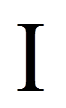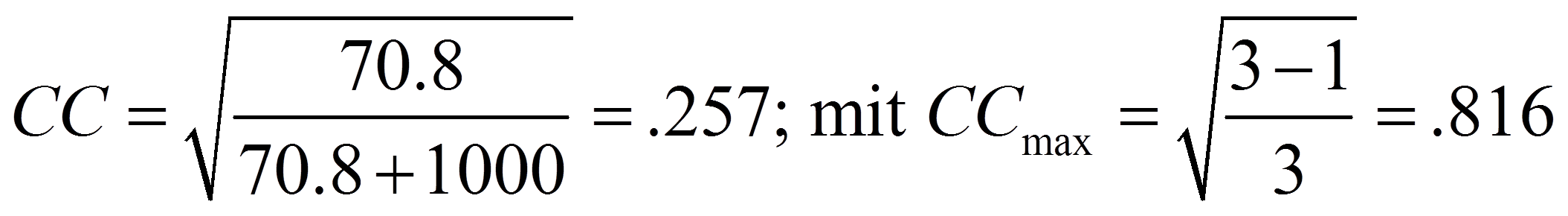Pearson Chi-Quadrat-Test (Kontingenzanalyse)
Seiteninhalt
- Quick Start
- 1. Einführung
- 1.1. Beispiele für mögliche Fragestellungen
- 1.2. Voraussetzungen
- 2. Grundlegende Konzepte
- 2.1. Beispiel einer Studie
- 2.2. Berechnung der Teststatistik
- 2.3. Zusammenhangsmasse
- 3. Der Pearson Chi-Quadrat-Test mit SPSS
- 3.1. SPSS-Befehle
- 3.2. Deskriptive Ergebnisse
- 3.3. Pearson Chi-Quadrat-Test
- 3.4. Zusammenhangsmasse
- 3.5. Eine typische Aussage
Quick Start
1. Einführung
Der Pearson Chi-Quadrat-Test testet, ob zwischen zwei kategorialen Variablen ein Zusammenhang besteht. Dabei werden die beobachteten Häufigkeiten mit theoretisch erwarteten Häufigkeiten verglichen. Danach werden die Stärke und die Richtung des Zusammenhangs ermittelt.
Dieser Chi-Quadrat-Test wird auch als "Kontingenzanalyse" bezeichnet und auch wenn von "Kreuztabellen" gesprochen wird, kommt meist dieser Test zum Zuge.
Die Fragestellung des Pearson Chi-Quadrat-Tests wird oft so verkürzt:
"Gibt es einen Zusammenhang zwischen zwei kategorialen Variablen? Falls ja, wie stark ist dieser Zusammenhang?"
1.1. Beispiele für mögliche Fragestellungen
- Hören Hunde besser auf ihren Namen, nachdem sie in einem Training Hundekekse, Streicheleinheiten oder ausschliesslich verbales Lob erhalten haben?
- Welchen Musikstil bevorzugen verschiedene Altersgruppen?
- Gibt es einen Zusammenhang zwischen der Parteipräferenz und dem Abstimmungsverhalten?
- Gibt es einen Zusammenhang zwischen dem Gesundheitsstatus (gesund, leichte Erkrankung, schwere Erkrankung, chronische Erkrankung) und dem gewählten Krankenkassenmodell?
1.2. Voraussetzungen
| ✓ | Die Variablen sind kategorial (nominal- oder ordinalskaliert) |
| ✓ | Die Stichprobe ist > 50. Ist dies nicht der Fall, so wird bei einer Stichprobe kleiner als 20 der exakte Test nach Fisher verwendet und bei einer Stichprobengrösse zwischen 20 und 50 die Korrektur nach Yates. |
| ✓ | Die erwarteten Zellhäufigkeiten sind > 5. Ist dies nicht der Fall, so wird der exakte Test nach Fisher verwendet. |
| ✓ | Die Freiheitsgrade des Chi-Quadrat-Tests sind grösser als 1. Ist dies nicht der Fall, so wird die Korrektur nach Yates verwendet. |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
Ein Schweizer Detailhändler gibt eine Umfrage in Auftrag. Es soll herausgefunden werden, ob die Absatzmenge einer bestimmten Schokoladensorte durch die regional unterschiedlichen ökonomischen, sozialen und kulturellen Gegebenheiten beeinflusst wird. Dazu werden 1'000 Personen in den Regionen Zürich, Genf und Tessin gefragt, wie viele Packungen sie pro Monat kaufen. Die entsprechende Variable "Kaufmenge" hat drei Ausprägungen "0-1", "2-3" und "4 und mehr". Es stellt sich die Frage: Gibt es einen Zusammenhang zwischen Region und Kaufmenge?
Der zu analysierende Datensatz enthält neben einer Befragtennummer (ID) die Region, in welcher die Befragung stattgefunden hat (Region), sowie die Kaufmenge (Kaufmenge).
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Berechnung der Teststatistik
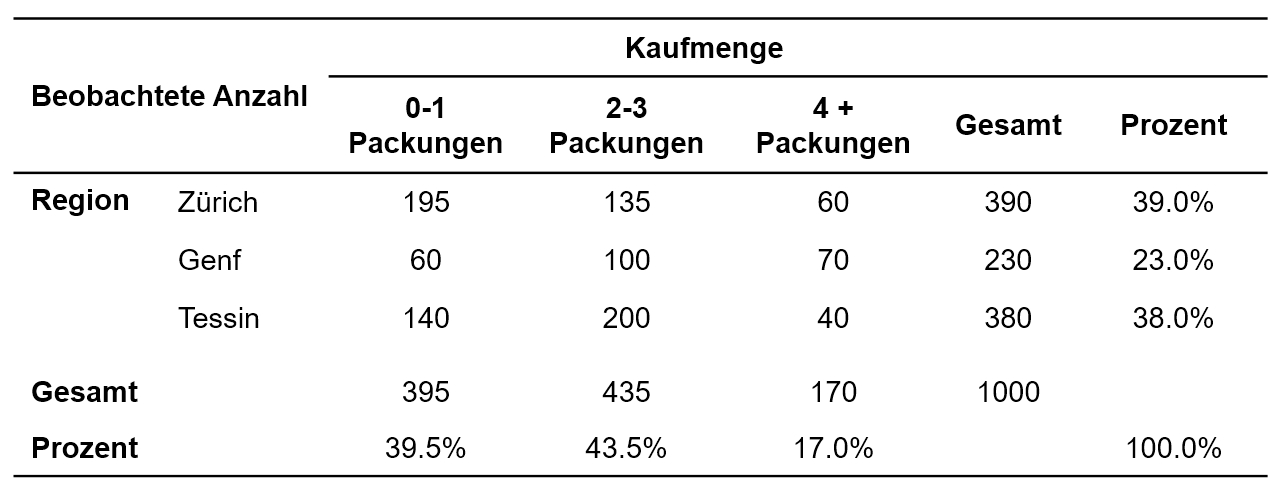
Beobachtete und erwartete Häufigkeiten
Im Rahmen der Kontingenzanalyse werden beobachtete und erwartete Häufigkeiten verglichen. Die beobachteten Häufigkeiten des Beispiels können Abbildung 1 entnommen werden. Die erwarteten Häufigkeiten werden mit Hilfe der sogenannten "Randverteilung" der Tabelle der beobachteten Häufigkeiten bestimmt. Als "Randverteilung" werden die Zeilen- und Spaltensummen der Kreuztabelle bezeichnet. In Abbildung 1 sind dies die Reihe und die Spalte "Gesamt". In der Zeile und der Spalte "Prozent" ist die Randverteilung zudem in Prozenten angegeben.
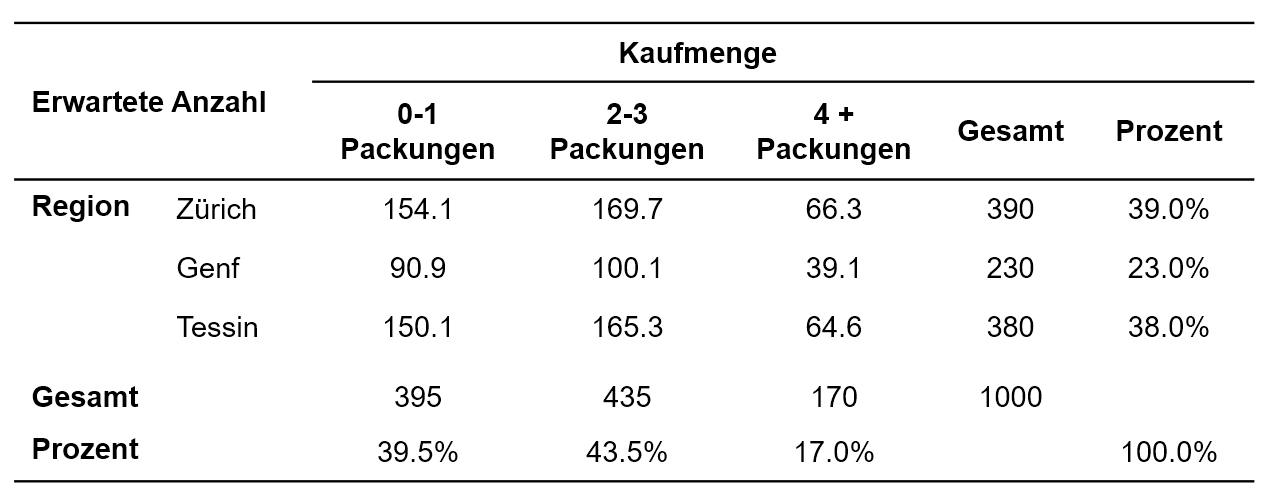
Mit Hilfe der Randverteilung werden jene Häufigkeiten berechnet, die aufgrund der Randverteilung in den Zellen erwartet würden, gegeben die beiden Merkmale – hier Region und Kaufmenge – sind voneinander unabhängig. Dazu wird für jede Zelle der zugehörige Spaltenwert der Randverteilung mit dem zugehörigen Zeilenwert der Randverteilung multipliziert und durch die Stichprobengrösse dividiert. Beispielsweise um den erwarteten Wert in Zürich mit einer Kaufmenge von 0-1 Packungen zu errechnen, wird gerechnet 395 * 390 / 1000 = 154.1. Alternativ kann mit Prozentwerten gerechnet werden, dann wird jedoch mit der Stichprobengrösse multipliziert (statt dividiert): 39.5% * 39.0% * 1000 = 154.1. Dies heisst, es wird geschaut, welcher Anteil der Stichprobe 0-1 Packungen kauft (39.5%) und welcher Anteil der Stichprobe in Zürich befragt wurde (39.0%). Aus der Kombination dieser beiden Informationen wird errechnet, welcher Wert erwartet wird. Abbildung 2 zeigt die erwarteten Häufigkeiten des Beispiels.
Berechnen der Teststatistik
Werden nun die beobachteten und die erwarteten Werte verglichen (Abbildung 1 und Abbildung 2), so zeigen sich für das Beispiel deutliche Unterschiede. Ob diese jedoch signifikant sind, wird mittels Chi-Quadrat-Test geprüft. Dessen Teststatistik berechnet sich wie folgt:
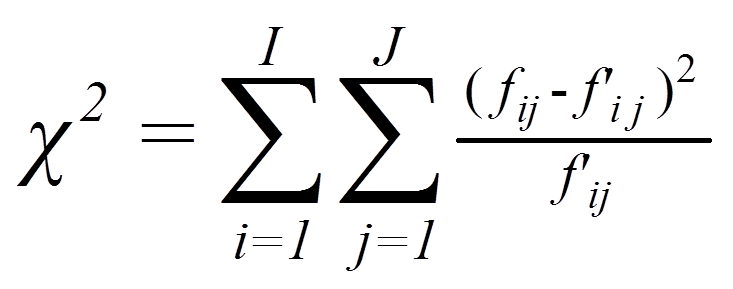
mit
|
|
= | beobachtete Häufigkeit in einer Zelle |
|
|
= | erwartete Häufigkeit in einer Zelle |
|
|
= | Laufindex über Spalten (I = Anzahl Spalten) |
|
|
= | Laufindex über Zeilen (J = Anzahl Zeilen) |
Für das vorliegende Beispiel ergibt dies:
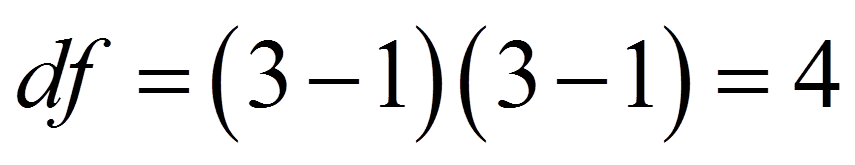
Signifikanz der Teststatistik
Um zu prüfen, ob die Abweichung zwischen beobachteten und erwarteten Häufigkeiten signifikant ist, wird die Teststatistik mit dem kritischen Wert der durch die Freiheitsgrade (df) bestimmten Chi-Quadrat-Verteilung verglichen. Dieser kritische Wert kann Tabellen entnommen werden. Abbildung 3 zeigt einen Auszug.
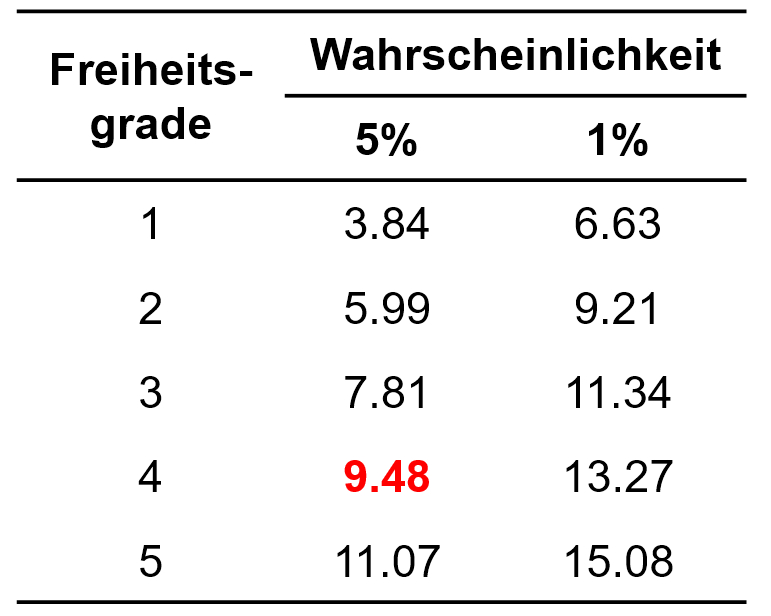
Für das vorliegende Beispiel beträgt der kritische Wert 9.48 bei df = 4 und α = .05 (siehe Abbildung 3). Ist der Wert der Teststatistik höher als der kritische Wert, so ist der Unterschied signifikant. Dies ist für das Beispiel der Fall (70.8 > 9.48). Daher kann davon ausgegangen werden, dass sich die erwarteten und die beobachteten Häufigkeiten signifikant unterscheiden (Chi-Quadrat(4) = 70.8, p < .001, n = 1000).
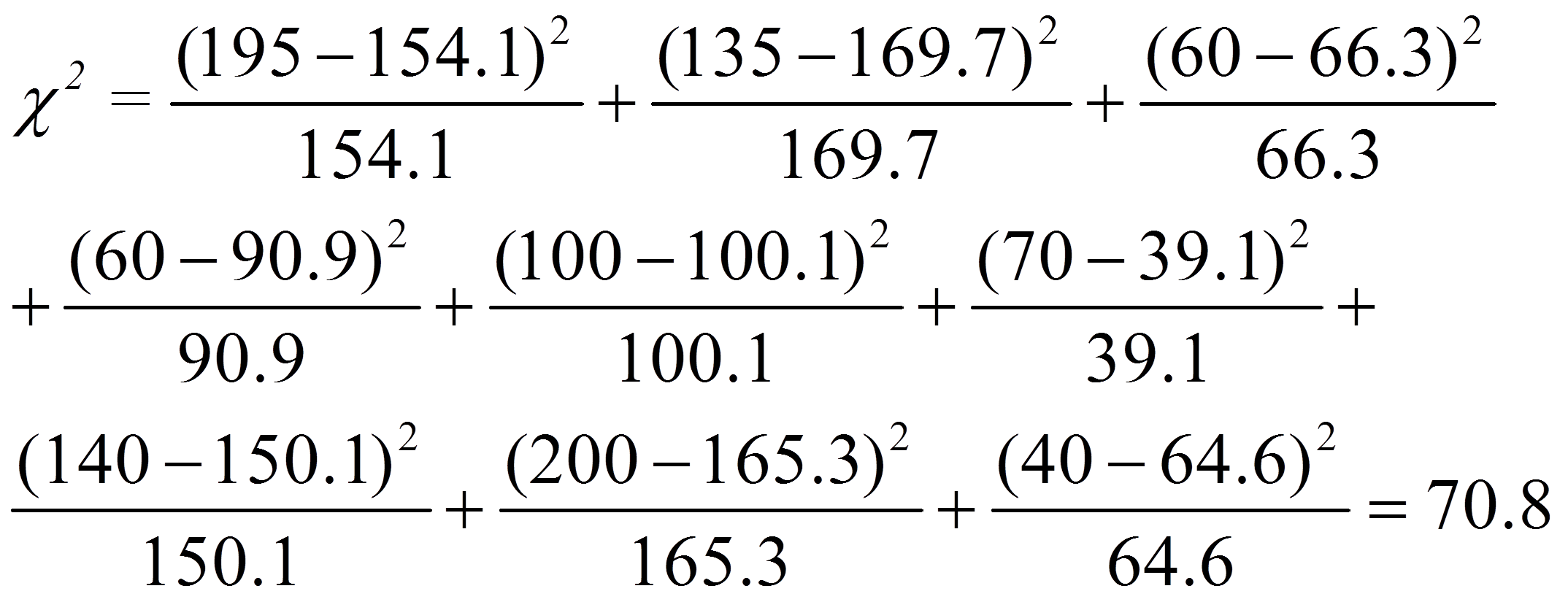
Die Freiheitsgrade berechnen sich wie folgt:
df = (Anzahl Variablenstufen Region - 1) x (Anzahl Variablenstufen Kaufmenge - 1)
Die Korrektur nach Yates
Ist df = 1, so wird empfohlen, die Korrektur von Yates zu verwenden. Die Korrektur von Yates subtrahiert von jedem Summanden des Chi-Quadrat-Tests 0.5, so dass die Chi-Quadrat-Statistik geringer ausfällt und der Test damit konservativer wird (i.e. die Differenzen müssen grösser sein, damit der Test signifikant ausfällt).
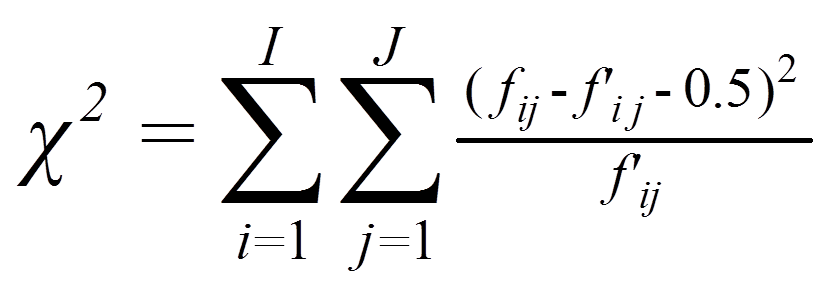
mit
|
|
= | beobachtete Häufigkeit |
|
|
= | erwartete Häufigkeit |
|
|
= | Laufindex über Spalten (I = Anzahl Spalten) |
|
|
= | Laufindex über Zeilen (J = Anzahl Zeilen) |
Für das Beispiel wird keine Korrektur angewandt, da die Stichprobe hinreichend gross ist und df = 4.
Der exakte Test nach Fisher
Ist die Stichprobengrösse n ≤ 20 oder es liegen erwartete Zellhäufigkeiten ≤ 5 vor, so wird die Anwendung des exakten Tests nach Fisher empfohlen. Bei zu geringen erwarteten Werten können auch Zeilen oder Spalten zusammengelegt werden, doch ist aus inhaltlichen Gründen in der Regel davon abzuraten. Der exakte Test nach Fisher basiert auf Simulationen und kennt keine Voraussetzungen. Daher kann er auch bei sehr kleinen Stichproben und geringen erwarteten Häufigkeiten eingesetzt werden. Für weitere Informationen sei an dieser Stelle auf Statistiklehrbücher verwiesen. Für das Beispiel kann auf die Berechnung des exakten Tests verzichtet werden, da die Stichprobe hinreichend gross ist und alle erwarteten Häufigkeiten > 5 sind (siehe Abbildung 2).
2.3. Zusammenhangsmasse
Um die Stärke des Zusammenhangs zu quantifizieren, liegen zwei Gruppen von Zusammenhangsmassen vor. Dies sind einerseits die "symmetrischen" Masse, anderseits die "Richtungsmasse". Welche Masse berichtet werden hängt einerseits von der wissenschaftlichen Community ab, andererseits aber auch von der Skalierung der Variablen. Für alle diese Masse wird geprüft, ob sich ihre Werte signifikant von 0 unterscheiden. Je weiter sie von 0 abweichen, desto grösser die Effektstärke. Auf eine Erläuterung dieser Tests wird jedoch verzichtet. Hier werden lediglich einige zentrale symmetrische Masse für Zusammenhänge zwischen zwei nominalen Variablen oder einer nominalen und einer ordinalen Variablen vorgestellt.
Die symmetrischen Masse geben Auskunft über die Stärke eines Zusammenhangs. Sie werden als "symmetrisch" bezeichnet, da es keine Rolle spielt, welche Variable die Spalten- und welche die Zeilenvariable ist. Die symmetrischen Masse basieren auf der Teststatistik Chi-Quadrat. Die drei wichtigsten Masse für nominalskalierte Variablen (oder eine nominale und eine ordinale Variable) sind Phi, Cramers V und der Kontingenzkoeffizient. Sie alle werden gelegentlich verwendet, wenngleich Cramers V das verbreitetste ist.
Phi (ϕ) ist ausschliesslich für 2x2-Tabellen geeignet und berechnet sich wie folgt:
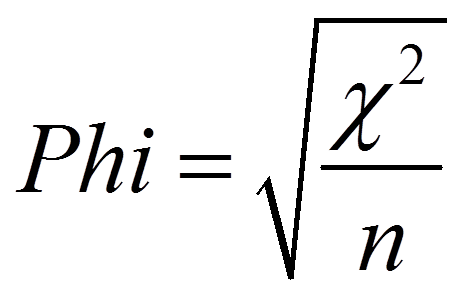
mit
|
|
= | Stichprobengrösse |
Für 2x2-Tabellen variiert Phi zwischen 0 und +1. Je weiter Phi von 0 entfernt, desto enger der Zusammenhang. Ist die Tabelle grösser als 2x2, so liegt das Maximum über 1 und der Koeffizient ist daher schwieriger zu interpretieren.
Cramers V und der Kontingenzkoeffizient stellen Adaptionen des Phi-Koeffizienten für grössere Tabellen dar. Während der Kontingenzkoeffizient ausschliesslich für quadratische Tabellen (z.B. 3x3, 4x4, 5x5) empfohlen wird, wird Cramers V für jegliche Tabellengrössen verwendet. Der Kontingenzkoeffizient (engl. "Contingency Coefficient", daher kurz CC) wird folgendermassen berechnet:
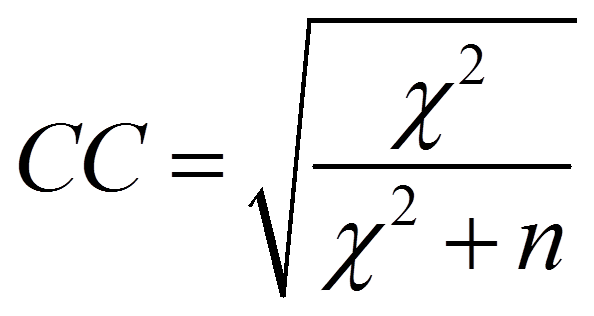
Der Kontingenzkoeffizient nimmt Werte zwischen 0 und einem Maximalwert an, welcher geringer als 1 ist und durch die folgende Formel bestimmt werden kann:
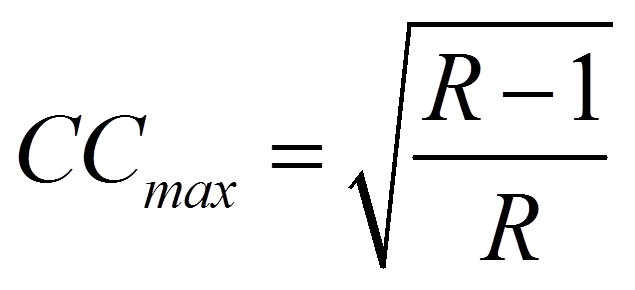
mit
|
|
= | min(I,J) |
|
|
= | Anzahl Spalten |
|
|
= | Anzahl Zeilen |
Cramers V weist den Vorteil auf, dass der Index Werte bis 1 erreichen kann ungeachtet der Tabellengrösse. Er ist für 2x2-Tabellen identisch mit Phi und wird folgendermassen berechnet:
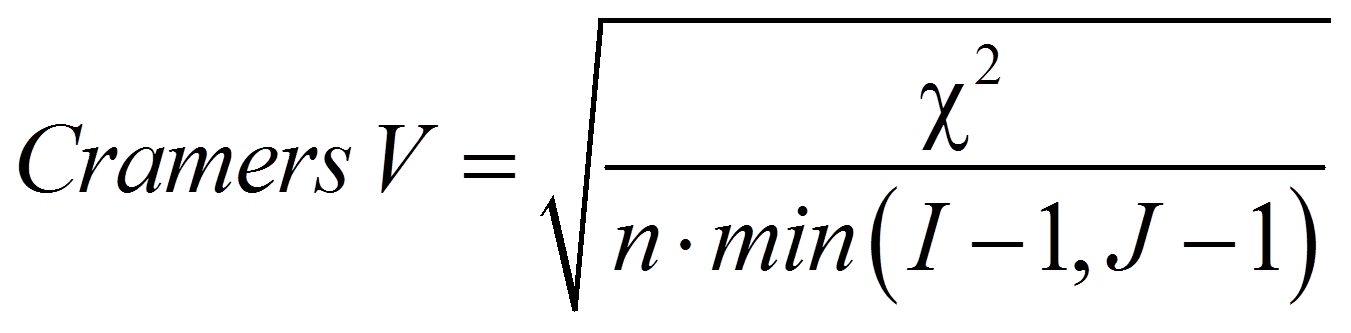
mit
|
|
= | Stichprobengrösse |
|
|
= | Anzahl Spalten |
|
|
= | Anzahl Zeilen |
Oft wird ab V ≥ .30 von einem "starken" Zusammenhang gesprochen.
Das vorliegende Beispiel ist eine 3x3-Tabelle. Daher könnten der Kontingenzkoeffizient und Cramers V verwendet werden. Für das vorliegende Beispiel errechnen sich Cramers V und der Kontingenzkoeffizient CC wie folgt:
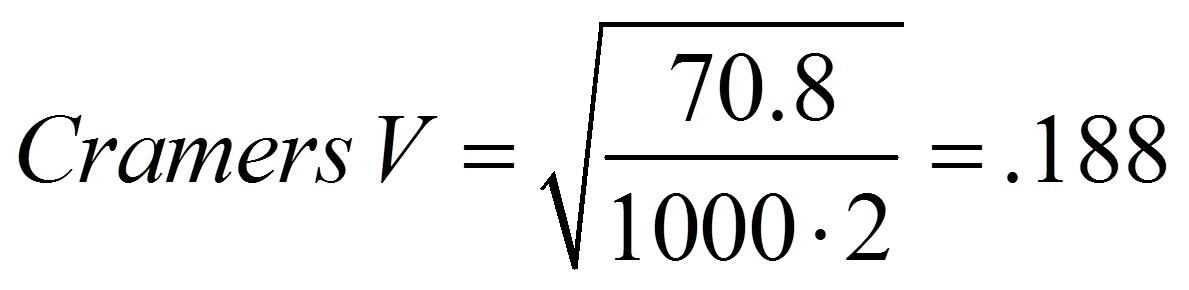
3. Der Pearson Chi-Quadrat-Test mit SPSS
3.1. SPSS-Befehle
SPSS-Menü: Analysieren > Deskriptive Statistiken > Kreuztabellen
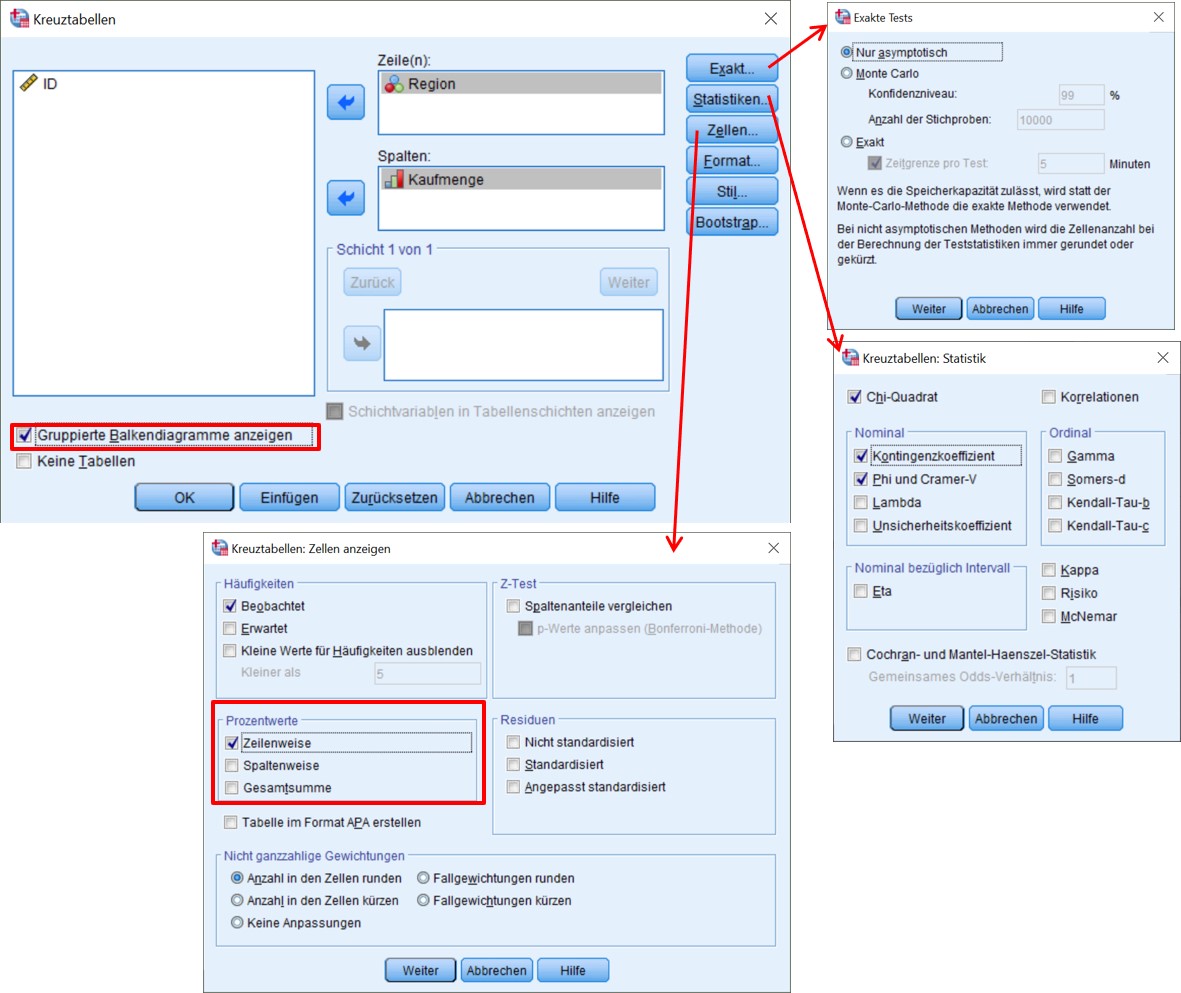
Hinweise
- Bei Stichproben < 20 oder erwarteten Häufigkeiten ≤ 5 wird Exakt gewählt.
- Chi-Quadrat muss gewählt werden für den Chi-Quadrat-Test.
- Zusammenhangsmasse werden in Abhängigkeit von Skalenniveau und Tabellengrösse gewählt.
SPSS-Syntax
CROSSTABS
/TABLES=Region BY Kaufmenge
/FORMAT=AVALUE TABLES
/STATISTICS=CHISQ CC PHI
/CELLS=COUNT ROW
/COUNT ROUND CELL
/BARCHART.
Es spielt für das statistische Ergebnis keine Rolle, welche Variable als Zeilenvariable und welche als Spaltenvariable verwendet wird.
Wie bereits erläutert, wird bei Stichproben kleiner als 20 sowie bei erwarteten Zellhäufigkeiten kleiner gleich 5 der exakte Test nach Fisher verwendet. Dazu wird bei Exakt "Exakt" angewählt. Die Stichprobengrösse ist in der Regel vor der Analyse bekannt, während zu geringe erwartete Häufigkeiten in der Regel erst bei der Beurteilung des SPSS-Outputs erkannt werden und die Analyse anschliessend erneut mit der Wahl von "Exakt" durchgeführt wird.
Bei einer 2x2-Tablle sowie Stichproben zwischen 20 und 50 wird die Korrektur von Yates empfohlen (in SPSS als "Kontinuitätskorrektur" bezeichnet). Diese kann in SPSS nicht angefordert werden, wird aber bei 2x2-Tabellen automatisch ausgegeben. Soll sie aufgrund der Stichprobengrösse verwendet werden, so müsste die Korrektur manuell vollzogen werden.
Die Zusammenhangsmasse werden wie erläutert in Abhängigkeit von Skalenniveau der beiden Variablen und von der Tabellengrösse gewählt: Ist mindestens eine der Variablen nominal, so werden Masse in der Box "Nominal" verwendet. Sind beide Variablen ordinal, so werden Masse in der Box "Ordinal" verwendet. (Ist eine der Variablen nominal, die andere aber intervallskaliert, so empfiehlt es sich anstelle eines Chi-Quadrat-Tests ein anderes Verfahren anzuwenden – je nach Anzahl Ausprägungen der nominalen Variable und nach der Verteilung der intervallskalierten Variable einen t-Test für unabhängige Gruppen, einen Mann-Whitney-U-Test, eine einfaktorielle Varianzanalyse oder einen Kruskal-Wallis-Test.)
Die Ausgabe von Prozentwerten in der Kreuztabelle dient lediglich deskriptiven Zwecken. Einerseits werden die Prozentwerte gelegentlich für die Berichterstattung verwendet, andererseits erleichtern sie den Vergleich der Spaltenvariable für verschiedene Werte der Zeilenvariable (oder umgekehrt). Für die Beispieldaten wurden Zeilenprozente gewählt aufgrund der Verwendung der Region als Zeilenvariable und der Kaufmenge als Spaltenvariable. So wird die prozentuale Aufteilung der Einkäufe innerhalb jeder Region gezeigt und die Regionen können trotz Unterschieden in den absoluten Zahlen (230 Befragte in Genf, 390 in Zürich etc.) relativ einfach verglichen werden.
3.2. Deskriptive Ergebnisse
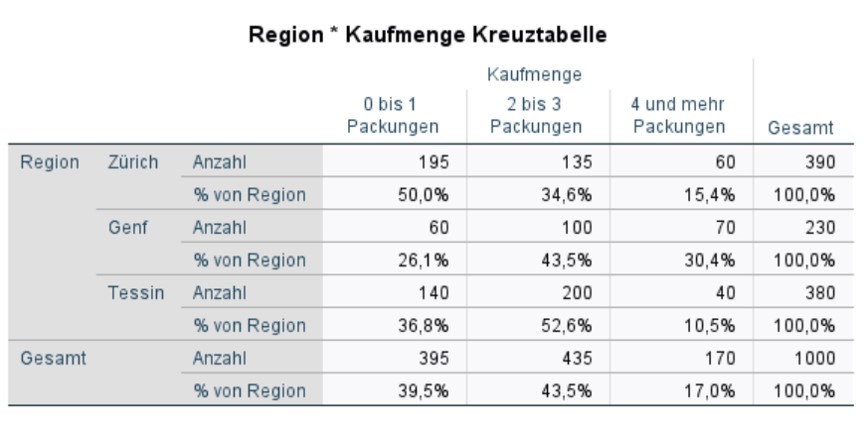
Abbildung 5 zeigt die Kreuztabelle der beiden Variablen mit den angeforderten Zeilenprozentwerten. Abbildung 6 zeigt ein für die Zeilenvariable gruppiertes Balkendiagramm, das dieselben Informationen zusammengefasst grafisch veranschaulicht. Beide Darstellungsweisen führen in der Regel zu den gleichen Beobachtungen.
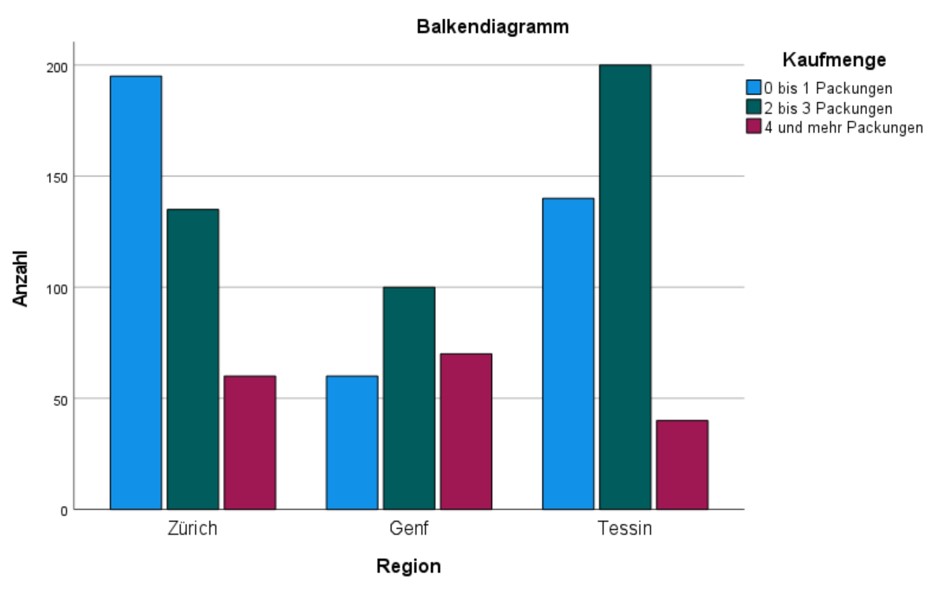
Bei der Interpretation eines derartigen Balkendiagramms muss berücksichtigt werden, dass es absolute Häufigkeiten darstellt. Daher sollten die absoluten Balkenlängen der verschiedenen "Gruppen" von Balken (Werte der Zeilenvariable, hier Regionen) nicht miteinander verglichen werden. In der Beispielstudie wurden beispielsweise in Genf lediglich 230 Personen befragt, während in Zürich 390 und im Tessin 380 Personen interviewt wurden. Stattdessen werden in diesem Diagramm die "Muster" der Regionen verglichen: Es zeigt sich, dass in Zürich die modale Kaufmenge 0-1 Packungen sind, während in Genf und im Tessin der Modus bei 2-3 Packungen liegt. In Genf scheint der Anteil der Konsumenten mit 2-3 Packungen vergleichsweise hoch. Damit scheinen also klare Unterschiede zwischen den Regionen vorzuliegen und es könnte also ein Zusammenhang zwischen Region und Kaufmenge bestehen. Ob dieser Zusammenhang signifikant ist, wird anhand des Chi-Quadrat-Tests entschieden.
3.3. Pearson Chi-Quadrat-Test
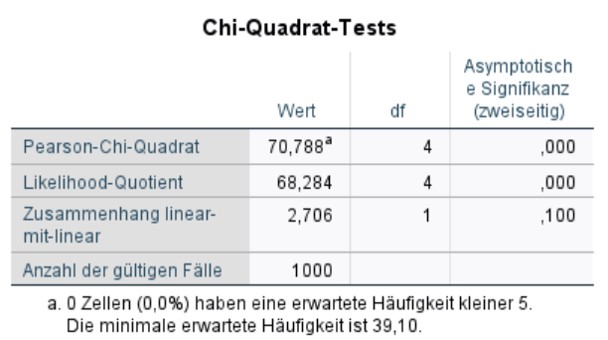
Der Chi-Quadrat-Test in Abbildung 7 bestätigt, dass ein Zusammenhang zwischen Region und Kaufmenge besteht (Chi-Quadrat(4) = 70.788, p < .001). Die Fussnote der Tabelle zeigt, dass keine erwarteten Zellhäufigkeiten kleiner als 5 vorliegen. Lägen zu geringe erwartete Häufigkeiten vor, so würde die Analyse wiederholt, wobei ein exakter Test nach Fisher angefordert würde.
3.4. Zusammenhangsmasse
Im vorliegenden Beispiel eignet sich Phi nicht als Zusammenhangsmass, da die Kreuztabelle grösser als 2x2 ist. Da die Tabelle aber quadratisch ist, eignen sich sowohl Cramers V als auch der Kontingenzkoeffizient CC. Diese beiden Masse werden darum berichtet.
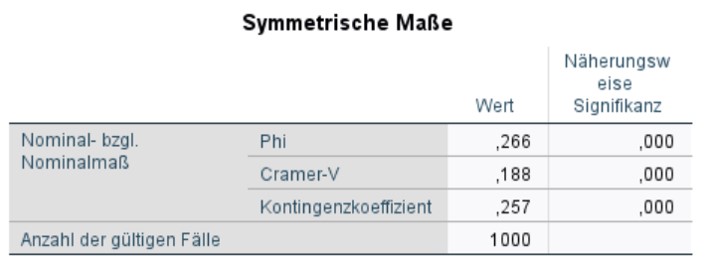
Wie Abbildung 8 entnommen werden kann, ist sowohl Cramers V (.188) als auch der Kontingenzkoeffizient CC (.257) signifikant (beide p < .001). Da die Werte jedoch unter .30 liegen, wird von einem nicht sehr starken Zusammenhang ausgegangen.
3.5. Eine typische Aussage
Die Einkaufsmengen von Schokolade und die Region, in der die befragten Personen wohnen, stehen in einem Zusammenhang (Chi-Quadrat(4) = 70.8, p = .000, n = 1000). Der Zusammenhang ist allerdings nicht sehr stark (CC = .257, p < .001; Cramers V = .188, p < .001).