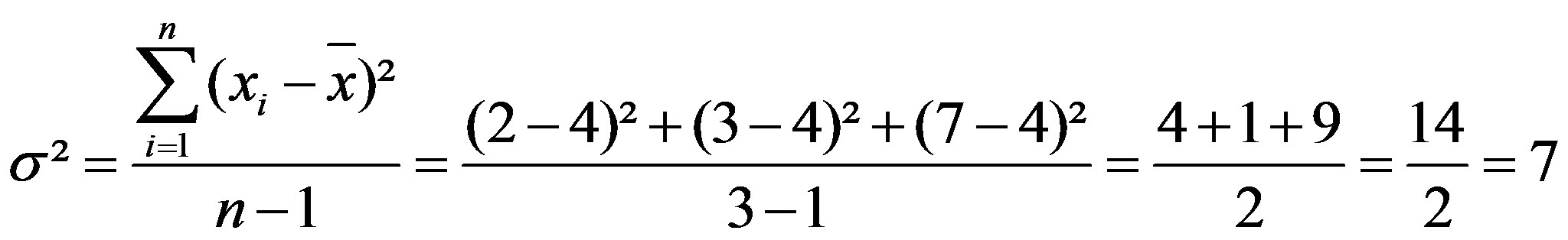Navigation auf uzh.ch
Navigation auf uzh.ch
Die univariate, deskriptive Analyse ist ein wichtiger Schritt im Rahmen jeder Datenanalyse. Sie dient einerseits der Beschreibung eines Datensatzes anhand einzelner Merkmale und hilft, mögliche Fehler bei der Datenerfassung und/oder Ausreisser im Datensatz zu entdecken. Andererseits ist sie notwendig, um die Eignung der Daten für bestimmte bi- und multivariate Analyseverfahren einzuschätzen. Im Rahmen dieses Schrittes werden in der Regel Häufigkeitsverteilungen sowie Lage- und Streuungsmasse betrachtet.
Häufigkeitsverteilungen beschreiben, wie oft die verschiedenen Merkmalsausprägungen einer Variablen im Datensatz vorkommen. Es wird dabei zwischen absoluten und relativen Häufigkeiten unterschieden: Die absolute Häufigkeit gibt an, wie häufig eine bestimmte Merkmalsausprägung im Datensatz vorkommt. Gibt es sehr viele verschiedene Merkmalsausprägungen im Datensatz, so fasst man sie oftmals zu Klassen zusammen. Dies macht die deskriptiven Ergebnisse übersichtlicher und dadurch leichter lesbar.
Beispielsweise ist es gelegentlich sinnvoll, Alters- oder Einkommensklassen zusammenzufassen. Manchmal werden auch aus inhaltlichen Gründen verschiedene Gruppen zusammengefasst, wie zum Beispiel Berufsgruppen oder wenn Antworten auf eine offene Frage nach dem "Lieblingsmusiker" in Musikstile klassifiziert werden.
Die relative Häufigkeit zeigt, welcher relative Anteil der Untersuchungseinheiten eine bestimmte Merkmalsausprägung aufweist – zum Beispiel wie viel Prozent der Bevölkerung angibt, "eher umweltbewusst" oder "sehr umweltbewusst" zu sein oder welcher Anteil aller SchülerInnen eines Jahrganges eine genügende Testleistung erreicht haben.
Die Darstellung erfolgt durch Häufigkeitstabellen und/oder graphisch, beispielsweise durch Balken- oder Kreisdiagramme. Unter den graphischen Darstellungsformen werden für stetige Variablen Histogramme besonders häufig verwendet.
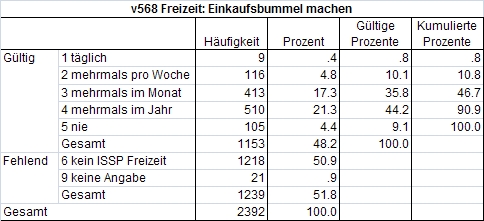
SPSS gibt Häufigkeitstabellen wie in Abbildung 1 aus. Darin ist ersichtlich, wie häufig die Personen angeben, "einen Einkaufsbummel" zu unternehmen (Quelle Daten: Allbus 2008, nur Westdeutsche). Die Ausgabe einer Häufigkeitstabelle für jede Variable ist vor der Durchführung von statistischen Tests notwendig. Anhand einer solchen Tabelle lässt sich schnell erkennen, ob Werte irrtümlicherweise falsch eingegeben wurden. Das Histogramm in Abbildung 2 veranschaulicht denselben Sachverhalt, allerdings ohne Berücksichtigung der fehlenden Werte:
Am Histogramm lassen sich leicht Ausreisser erkennen. Die Verteilung lässt sich grundsätzlich beschreiben durch die Anzahl Modi ("Gipfel"), deren Aussehen und die Symmetrie oder Asymmetrie des Histogramms. Diese Charakteristika der Verteilung können auch numerisch erfasst werden durch die sogenannten Verteilungsparameter.
Zusätzlich zu einer graphischen Darstellung lassen sich verschiedene Parameter berechnen, welche die Verteilung der Merkmalsausprägungen charakterisieren. Dazu gehören Lage- und Streuungsparameter. Alle beschriebenen Parameter lassen sich mit SPSS im Dialogfenster "Häufigkeiten" berechnen. Hierzu müssen die zu berechnenden Parameter unter "Statistiken" ausgewählt werden. Bei intervallskalierten Variablen werden im Ergebnisbericht immer Mittelwert und Varianz bzw. Standardabweichung angegeben.
Lagemasse beschreiben die sogenannte zentrale Tendenz der Daten. Diese charakterisieren die Häufigkeitsverteilung durch einen einzigen Wert, der die gesamte Verteilung so gut wie möglich repräsentieren soll. Wichtige Masse sind das arithmetische Mittel, der Median und der Modus.
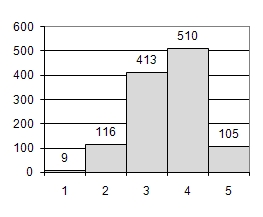
Das arithmetische Mittel (Mittelwert, engl. "mean") ist das gebräuchlichste Mass der zentralen Tendenz. Es ist identisch mit dem mathematischen Durchschnitt. Hier ein Berechnungsbeispiel:
x1 = 2; x2= 3; x3 = 7
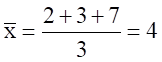
Zur Berechnung des Mittelwertes ist prinzipiell ein metrisches Skalenniveau erforderlich. In der Praxis wird es allerdings häufig auch auf der Basis ordinalskalierter Daten errechnet (zum Beispiel bei Likert-skalierten Items).
Der Median (Zentralwert, engl. "median") teilt eine Stichprobe in zwei gleich grosse Hälften. Er ist damit das 50%-Quantil der Verteilung einer Variablen. Es liegen genau so viele Werte unter wie über diesem Wert. Mindestvoraussetzung ist ein ordinales Skalenniveau.
Bei einer geraden Anzahl Fälle ist der Modus im Falle metrischer Daten der arithmetische Mittelwert der beiden in der Mitte liegenden Fälle. Bei ordinalskalierten Daten wird der Median als zwischen den beiden mittleren Werten liegend berichtet. Sind die Daten klassiert, so wird in der Regel die Klasse als Median angegeben, die gemeinsam mit den davor liegenden Klassen 50% oder mehr aller Fälle erfasst. Dies ist im Beispiel in Abbildung 1 die Ausprägung 4 ("mehrmals im Jahr"), denn mit der Ausprägung 3 ("mehrmals im Monat") wird die "50%-Grenze" nicht überschritten. Dies lässt sich schnell anhand der Spalte "kumulierte Prozente" aus der Häufigkeitstabelle feststellen.
Während das arithmetische Mittel durch Ausreisser stark beeinflusst wird, ist der Median gegenüber Extremwerten robust, da er zur Bestimmung lediglich die Ränge der Beobachtungen, nicht aber deren absolute Ausprägungen berücksichtigt.
Der Modus (Modalwert, engl. "mode") ist der häufigste Wert einer Verteilung. Er wird vor allem bei nominalskalierten Daten verwendet, beispielsweise zur Bestimmung der häufigsten Hunderasse. Im Beispiel zur Häufigkeit von Einkaufsbummeln wäre der Modus die Ausprägung 4 ("mehrmals im Jahr"). Dies lässt sich sehr schnell anhand der Häufigkeitstabelle (Abbildung 1) und des Histogramms (Abbildung 2) erkennen.
Der Modus ist nicht eindeutig, falls mehrere Ausprägungen gleich häufig vorkommen. In diesem Fall werden beide Ausprägungen als Modi (Plural von Modus) genannt - die Verteilung ist bimodal - oder es wird im Falle von metrischen Daten der Mittelwert der beiden Ausprägungen berichtet. Der Modalwert wird insbesondere bei kleinen Stichproben oft von Zufallsschwankungen beeinflusst. Allgemein beinhaltet er nur die Information, welche Ausprägung am häufigsten vorkommt.
Die Streuungsparameter (Dispersionsmasse) beschreiben die Variabilität der Ausprägung eines Merkmals in einem Datensatz. Sie messen, wie dicht die Werte einer Häufigkeitsverteilung um den Mittelwert streuen. Die am häufigsten verwendeten Grössen sind die Varianz und die Standardabweichung. Beide erfordern theoretisch ein metrisches Skalenniveau.
Die Varianz (s2, engl. "variance") wird als durchschnittliche quadratische Abweichung der einzelnen Beobachtungswerte vom arithmetischen Mittel errechnet:
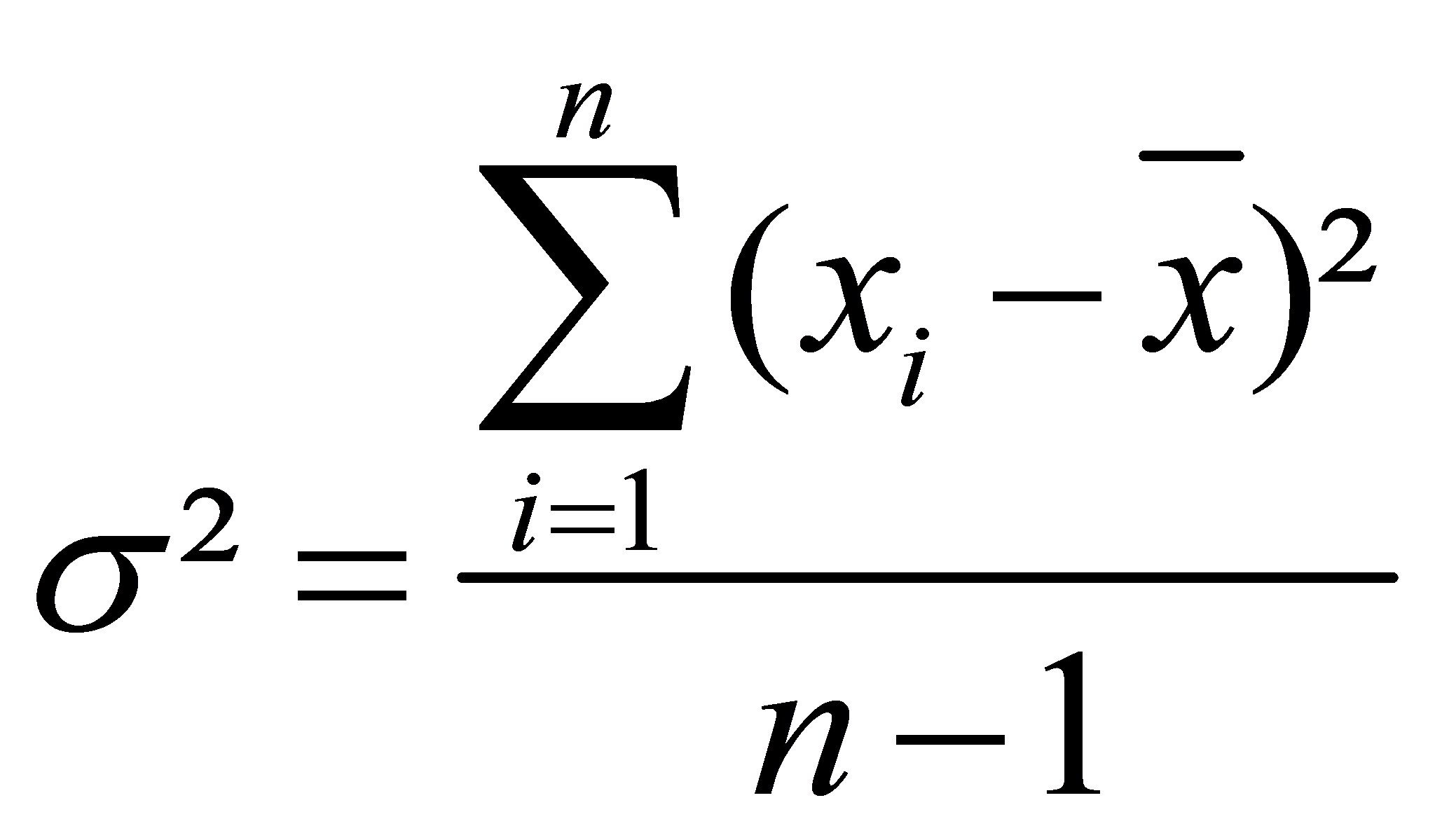
mit n = Anzahl Beobachtungen
Hier ein Berechnungsbeispiel:
x1 = 2; x2= 3; x3= 7; Mittelwert = 4
Die Standardabweichung (s, engl. "standard deviation", daher oft als "SD" abgekürzt) ist die Quadratwurzel der Varianz. Die Standardabweichung des obigen einfachen Beispiels errechnet sich wie folgt:
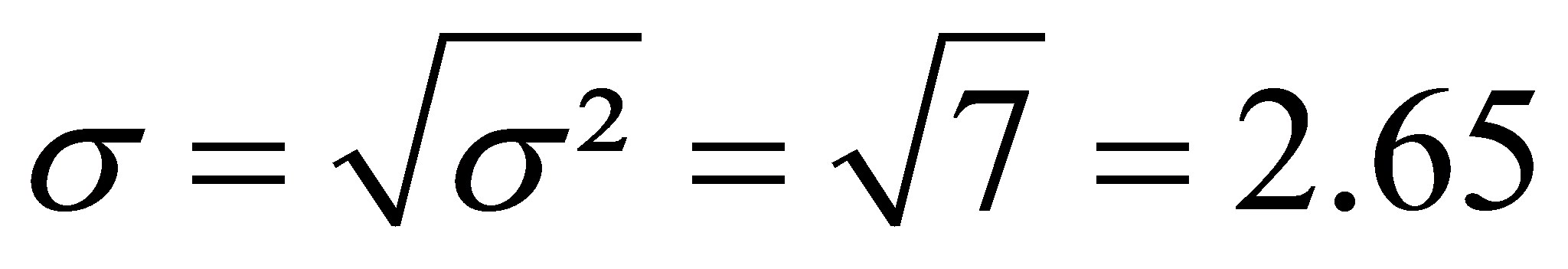
Der Vorteil der Standardabweichung gegenüber der Varianz ist, dass die Standardabweichung die gleiche Masseinheit wie die ursprüngliche Variable hat. Dies erleichtert die Interpretation des Wertes. So könnte beispielsweise ermittelt worden sein, dass die Schüler einer Klassenstufe durchschnittlich 33.8 Schulstunden in der Woche besuchen. Ein Varianzwert von 6.5 würde dann bedeuten, dass die Stundenzahlen um durchschnittlich 6.5 Quadratstunden um den Mittelwert streuen. Einfacher ist die Aussage mit der Standardabweichung: Die Schulstunden streuen um durchschnittlich 2.5 Stunden um den Mittelwert.
Sowohl bei der Standardabweichung als auch der Varianz fallen Ausreisser stark ins Gewicht. Auch aus diesem Grund sollte die Verteilung der Daten vor der Berechnung von Kennwerten oder Teststatistiken immer überprüft werden.
Die Schiefe (engl. "skewness") ist ein Mass für die Symmetrie einer Häufigkeitsverteilung. Meist lässt sich bereits anhand der Lage von Mittelwert, Median und Modus zueinander erkennen, ob und in welche Richtung eine Verteilung schief ist (im Vergleich zu einer Normalverteilung). Dazu kann jedoch auch eine spezifische Masszahl errechnet werden: die Schiefe. Sie kann in SPSS als Option des Befehls "Häufigkeiten" ausgegeben werden.
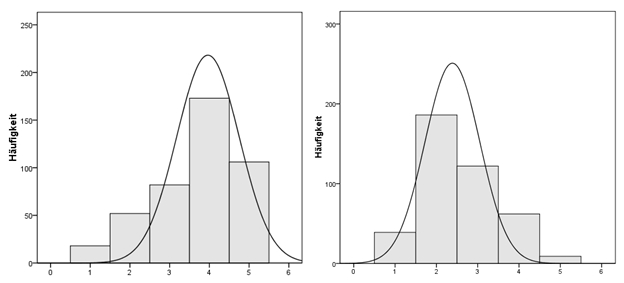
Die Verteilung in der linken Hälfte von Abbildung 3 ist eher linksschief. In diesem Fall ist der berechnete Wert für die Schiefe negativ. Ausserdem gilt folgende Faustregel für die Beziehung der drei Masse der zentralen Tendenz:
Mittelwert < Median < Modus
Die Verteilung in der rechten Hälfte von Abbildung 3 hingegen ist eher rechtsschief. In diesem Fall ist der berechnete Wert für die Schiefe positiv. Ausserdem gilt folgende Faustregel:
Mittelwert > Median > Modus
Bei einer Normalverteilung ist die Schiefe 0. Bei der Berechnung der Schiefe ist es wichtig zu beachten, dass dies nur bei so genannten unimodalen Verteilungsverläufen sinnvoll ist. "Unimodal" bedeutet, dass die Verteilung nur einen Modus hat. Es gibt aber auch Verteilungen, die mehr als einen Modus haben. Diese Verteilungen werden bei zwei Modi als "bimodal" bzw. bei zwei oder mehr Modi als "multimodal" bezeichnet. Vor der Berechnung der Schiefe sollte die Verteilung zunächst also in einem Histogramm betrachtet werden.
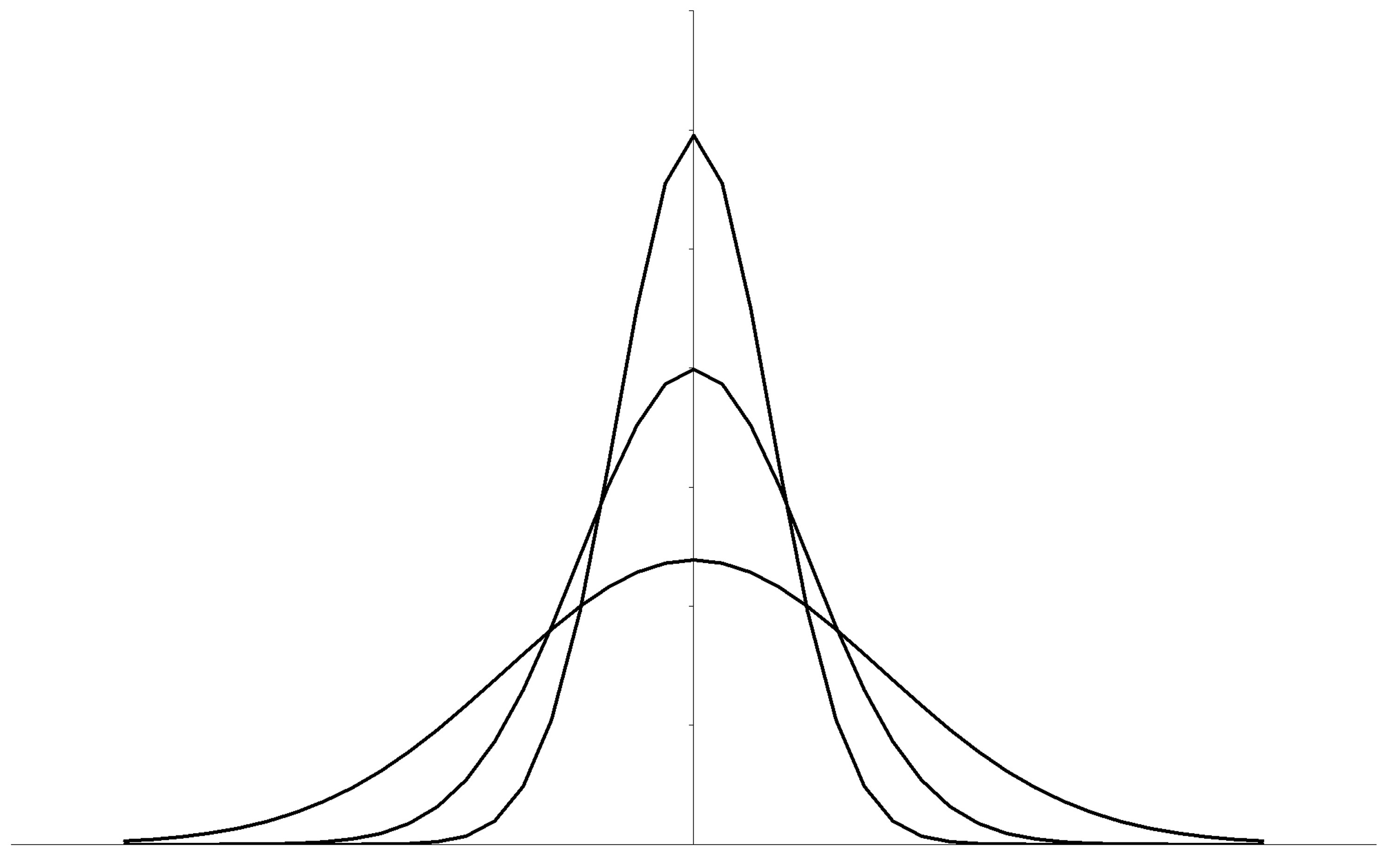
Die Kurtosis (Wölbung, Steilheit, Exzess, engl. "kurtosis") einer Verteilung drückt aus, ob die Verteilung im Vergleich zu einer Normalverteilung eher "schmalgipflig" oder "breitgipflig" ist. Bei gleichbleibender Standardabweichung können die Beobachtungen stärker auf die Mitte der Verteilung konzentriert vorliegen ("spitze" Verteilung) oder die Mitte ist eher wenig besetzt, was bei einer flachen Verteilung der Fall ist.
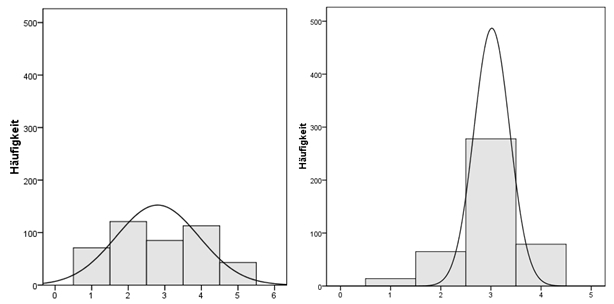
In Abbildung 4 weist das Histogramm links eine eher flache Verteilung auf. Hier ist der Wert für die Kurtosis negativ. Die Verteilung rechts ist dagegen eher steil, so dass der Wert für die Kurtosis positiv ist.
Bei einer Normalverteilung ist die Kurtosis 0. Wie bei der Berechnung der Schiefe ist auch bei der Berechnung der Kurtosis zunächst die Verteilung im Histogramm zu betrachten, damit sichergestellt werden kann, dass die Berechnung auch sinnvoll ist.
Als wichtigste Voraussetzung für die Durchführung von vielen statistischen Verfahren gilt neben der Forderung nach einem bestimmten Skalenniveau die annähernde Normalverteilung der Daten. Normalverteilungen sind theoretische Verteilungen, die von dem Mathematiker Gauß untersucht wurden und deshalb auch als "Gauß’sche Glockenkurven" bezeichnet werden.
Es gibt unendlich viele Normalverteilungen. Allen gemeinsam ist es, dass sie symmetrisch um den Mittelwert sind, "glockenförmig" sind und asymptotisch gegen 0 laufen. Die Schiefe ist somit immer Null. Ausserdem gilt, dass etwa 68% aller Messwerte innerhalb von einer Standardabweichung, 95% innerhalb von zwei Standardabweichungen und 99.7% aller Werte innerhalb von drei Standardabweichungen liegen. Aufgrund ihrer Eigenschaften reicht es aus, verschiedene Normalverteilungen anhand ihres Mittelwertes und der Varianz so N(μ; σ²) zu kennzeichnen, beispielsweise als N(5; 1.5). Normalverteilungen werden mit folgender Formel berechnet:
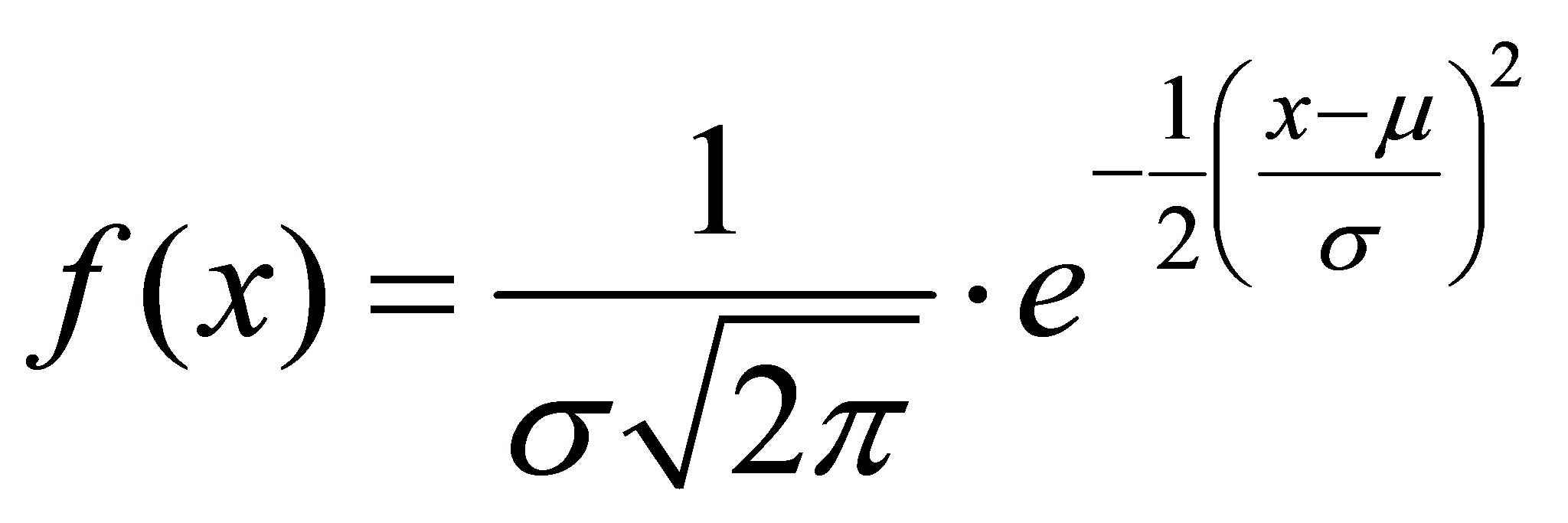
Setzt ein statistisches Verfahren also annähernd normalverteilte Daten voraus, so müssen die Daten vor dem Beginn auf eine Normalverteilung überprüft werden. Ist die Annahme zu stark verletzt, so muss ein Verfahren verwendet werden, das keine Normalverteilung voraussetzt. Die Daten lassen sich beispielsweise mit einem Chi²-Test auf Normalverteilung überprüfen.
Eine besondere Normalverteilung ist die sogenannte Standardnormalverteilung. Sie hat die Eigenschaft, dass ihr Zentrum auf der x-Achse bei 0 liegt. Ausserdem hat sie eine Varianz von 1. Sie wird durch folgende Formel abgebildet:
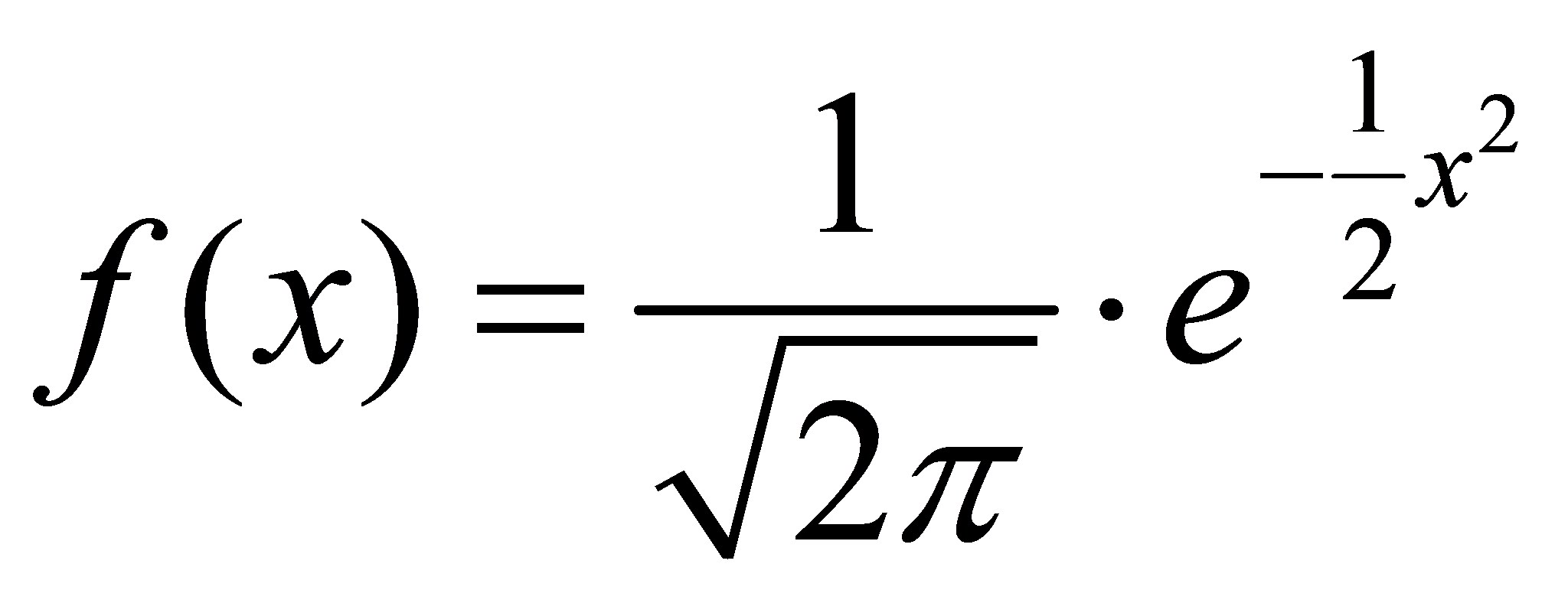
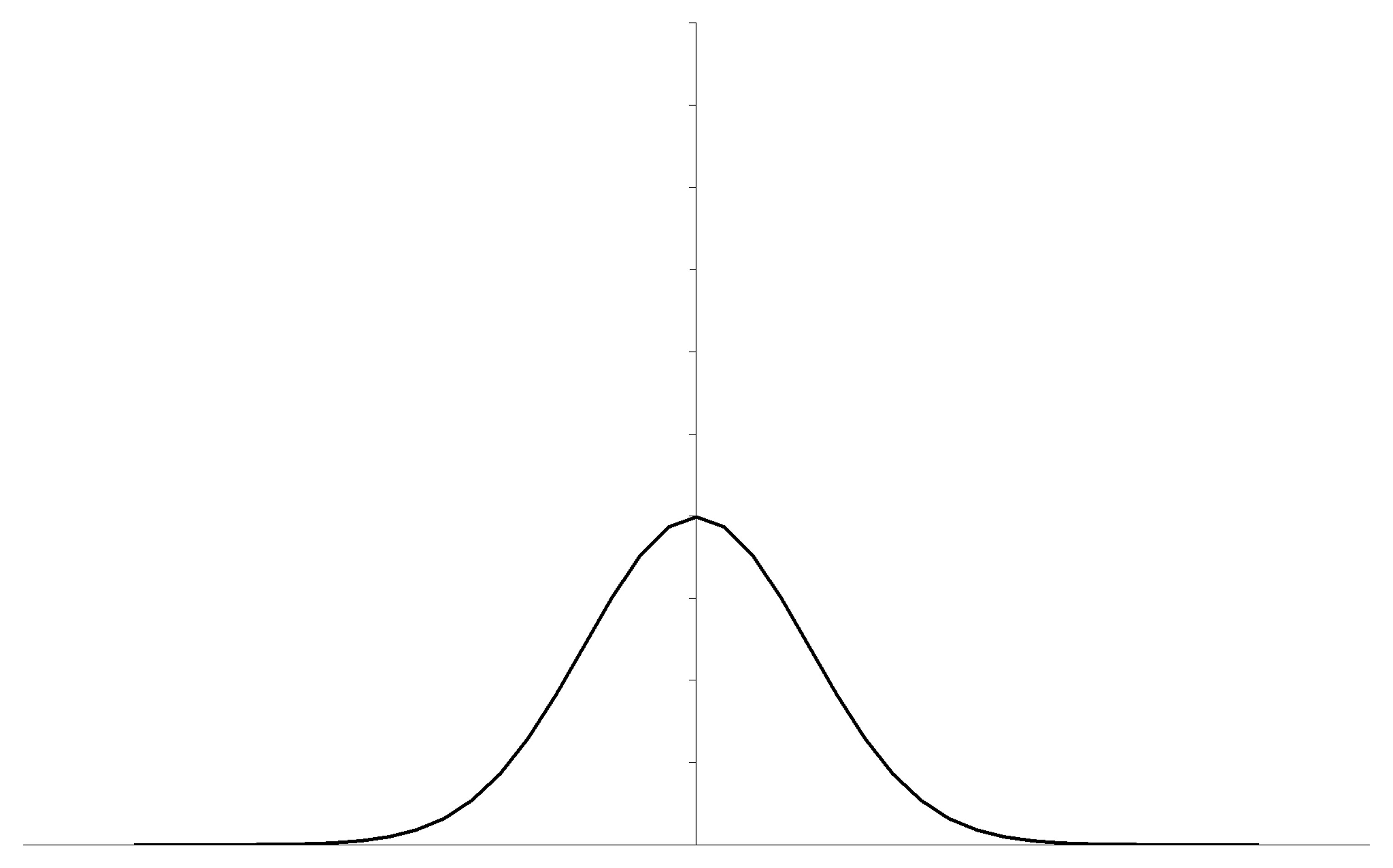
Jede Normalverteilung lässt sich durch Standardisierung in die Standardnormalverteilung überführen. Dies ist notwendig, wenn unterschiedlich verteilte Variablen miteinander verglichen werden sollen und wenn Verfahren angewandt werden, welche normalverteilte Daten voraussetzen.
Um die Werte einer Variablen zu standardisieren, wird folgende Formel verwendet:
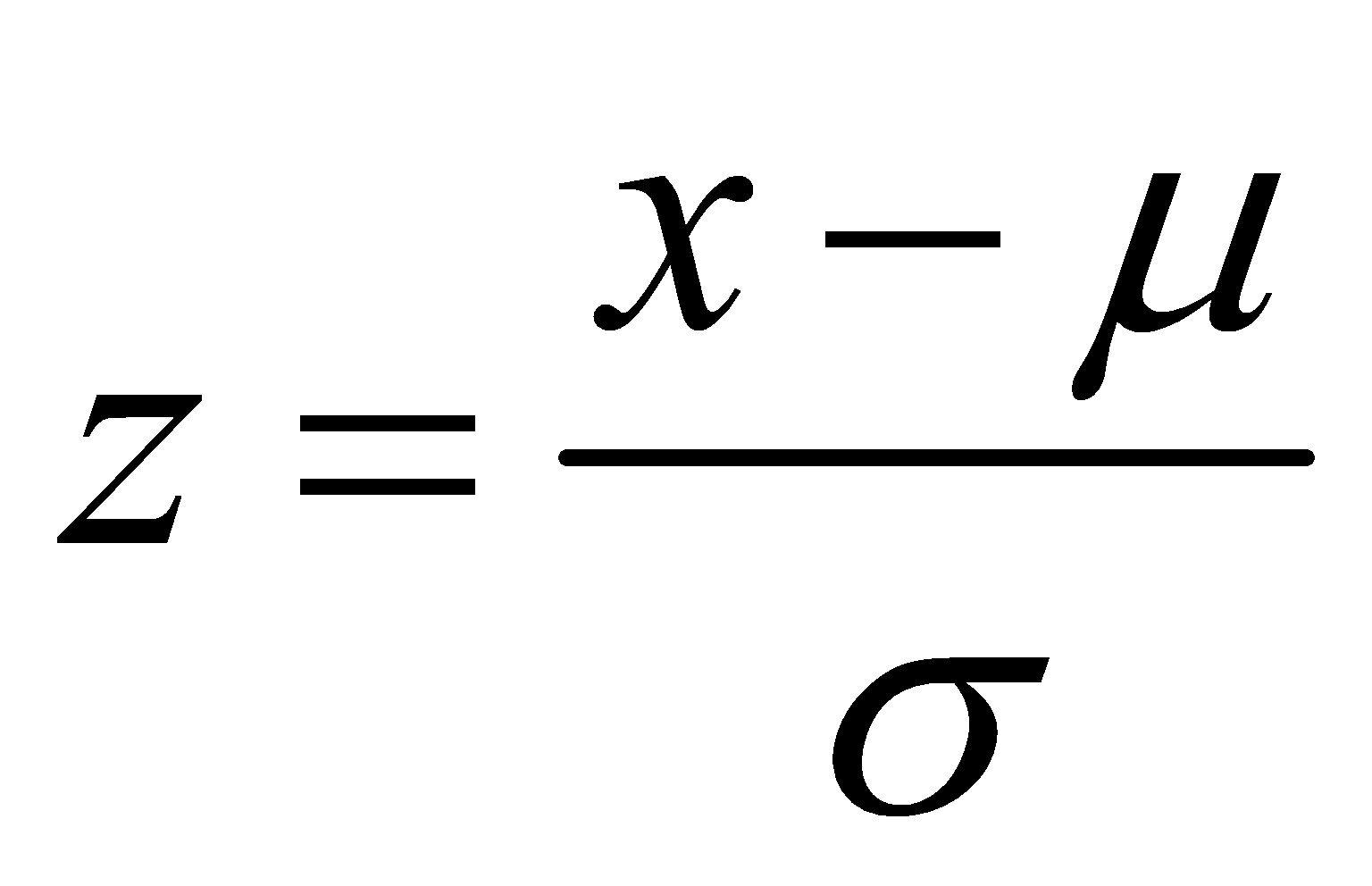
mit
n = Anzahl Beobachtungen
x = Merkmalsausprägung
μ = Mittelwert der Stichprobe
σ = Standardabweichung der Stichprobe
Für die standardisierten Werte wird üblicherweise der Buchstabe z verwendet. Aus diesem Grund wird auch von einer "z-Transformierung" gesprochen und die Werte werden als "z-Werte" bezeichnet.
